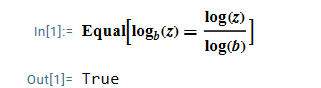Matematik- och fysikprovet 2022: Lösningsförslag

Plats för formelsamling och allmänna förslag och tips.

Formler, tips och tricks från detta prov: 

I våra lösningsförslag förekommer:

▢ Pythagoras sats

▢ Kvadreringsreglerna och konjugatregeln

▢ Kubreglerna: 

$$\begin{gathered} {\left(a+b\right)}^3=a^3+3a^{2}b+3a{b}^2+b^3 \\ {\left(a-b\right)}^3=a^3-3a^{2}b+3a{b}^2-b^3 \end{gathered}$$

▢ Konjugatregeln för kuber / Sum & difference of cubes:

$$\begin{gathered} a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right) \\ {a}^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right) \end{gathered}$$

▢ PQ-formeln

▢ $\sqrt{x^2}=\left|x\right|$

▢ Hantering av absolutbelopp

▢ Potenslagarna

▢ Logaritmlagarna

▢ Lösningar av trigonometriska ekvationer

▢ Trigonometriska ettan

▢ Dubbla vinkeln för sinus och cosinus

▢ Cosinussatsen

▢ Derivering av polynom, logaritmfunktioner, trigonometriska funktioner samt exponentialfunktioner

▢ Kedjeregeln, produktregeln och kvotregeln

▢ Gränsvärden, både mot ett värde och mot positiv/negativ oändlighet

▢ Geometriska summor

Metoder som används är exempelvis:

▢ Användning av enhetscirkeln

▢ Sambandet mellan en andragradsekvation på formen $x^2+px+q=0$ och dess rötter $x_1$ och $x_2$:

$\left\{\begin{array}{l}-\left(x_1+x_2\right)=p\\ x_1·x_2=q\end{array}\right.$

▢ Beräkningar med olikheter

▢ Användning av likformighet

▢ Beräkning gränsvärden, både från höger och från vänster, samt gränsvärden där en variabel går mot noll eller positiv/negativ oändlighet

Vad tas upp på MaFy-provet? 

MaFy-provets hemsida skriver följande om vad som prövas på matematikdelen av provet: 

• Hantering av algebraiska uttryck (potenser, rötter, polynom, rationella uttryck, kvadratkomplettering, faktorisering)
• Funktioner (polynom, rationella funktioner, exponential- och logaritmfunktioner, potensfunktioner, trigonometriska funktioner; derivator, deriveringsregler, derivatans koppling till växande/avtagande, lokala/globala extrema; enkla primitiva funktioner och integraler)
• Trigonometri (triangelsatserna; trigonometriska formler)
• Absolutbelopp
• Ekvationer och olikheter som involverar uttryck och funktioner av typerna listade ovan
• Geometri (kongruens, likformighet; rand- och medelpunktsvinklar; höjder, bisektriser och medianer i en triangel; Pythagoras sats och dess omvändning; koordinatgeometri)

Beskrivningarna inom parenteser är förstås inte uttömmande. Enstaka frågor av mer allmän karaktär eller utanför dessa områden kan förekomma.

Vad får jag ta med till provet? 

MaFy-provets hemsida skriver följande om vilka hjälpmedel som är tillåtna: 

Provdeltagare får bara ta med skrivmateriel. Skrivmateriel innebär tex pennor, suddgummi, passare och linjal. Högskolan tillhandahåller extra skrivpapper. Inga andra hjälpmedel är tillåtna om inte tillstånd har beviljats på grund av särskilda behov.

Med hjälp av en pappersbit och en passare kan en enkel gradskiva konstrueras. Det kan underlätta för att kontrollera rimligheten i en lösning vid behov. 

1. Om $a=\sqrt[3]{5}$, $b=\frac{1}{\sqrt[3]{5}}$ och $x=\frac{{\left(\sqrt{a}+\sqrt{b}\right)}^2-{\left(\sqrt{a}-\sqrt{b}\right)}^2}{ab}$ så gäller att x är lika med

(a): $\frac{2}{\sqrt[3]{5}}$

(b): $2\sqrt[3]{5}$

(c): 4

(d): inget av (a)-(c)

Börja med att förenkla täljaren genom att använda kvadreringsreglerna: 

$$\begin{gathered} x=\frac{\left({\sqrt{a}}^2+2\sqrt{a}\sqrt{b}+{\sqrt{b}}^2\right)-\left({\sqrt{a}}^2-2\sqrt{a}\sqrt{b}+{\sqrt{b}}^2\right)}{ab}= \\ \frac{\left(a+2\sqrt{a}\sqrt{b}+b\right)-\left(a-2\sqrt{a}\sqrt{b}+b\right)}{ab}=\frac{4\sqrt{a}\sqrt{b}}{ab}=\frac{4}{\sqrt{a}\sqrt{b}} \end{gathered}$$

Vi kan nu sätta in a och b:s värden: 

$x=\frac{4}{\sqrt{\sqrt[3]{5}}·\sqrt{{\displaystyle \frac{1}{\sqrt[3]{5}}}}}=\frac{4}{\sqrt{\bcancel{\sqrt[3]{5}}·{\displaystyle \frac{1}{\bcancel{\sqrt[3]{5}}}}}}=4$

Svar: (c), 4.

Tillägg: 10 apr 2023 15:02

Alternativ lösning (credit till Dracaena): 

Konjugatregeln lyder: $x^2-y^2=(x+y)(x-y)$. Det innebär att täljaren kan skrivas om: 

$$\begin{gathered} x=\frac{{\left(\sqrt{a}+\sqrt{b}\right)}^2-{\left(\sqrt{a}-\sqrt{b}\right)}^2}{ab}= \\ \frac{\stackrel{2\sqrt{a}}{\overbrace{\left(\left(\sqrt{a}+\sqrt{b}\right)+\left(\sqrt{a}-\sqrt{b}\right)\right)}}·\stackrel{2\sqrt{b}}{\overbrace{\left(\left(\sqrt{a}+\sqrt{b}\right)-\left(\sqrt{a}-\sqrt{b}\right)\right)}}}{ab}= \\ \frac{4\sqrt{ab}}{ab}=\frac{4}{\sqrt{ab}} \end{gathered}$$

Notera även att $ab=1$, eftersom b är inversen av a, dvs. $b=\frac{1}{a}$. Därmed är $x=\frac{4}{\sqrt{ab}}=\frac{4}{\sqrt{1}}=4$.

Svar: (c), 4.

Uppgifter som liknar denna:

1. Om $a=\sqrt{5}$, $b=\sqrt{2}$ och $x=\frac{\sqrt{b}\left(3a\sqrt{b}+2\right)-2\sqrt{b}}{a^2-b^2}$ så gäller att x är lika med

(a): $\sqrt{10}$

(b): 2

(c): $\frac{3\sqrt{10}}{2}$

(d): inget av (a)-(c)

2. Om $a=256$, $b=9$ och $x=\frac{\sqrt{a^{2}b}+2\sqrt[4]{{\left(ab\right)}^3}+\sqrt{a{b}^2}}{\sqrt{a}\sqrt{ab}-\sqrt{b}\sqrt{ab}}$, så gäller att x är lika med

(a): $\frac{4-\sqrt[4]{3}}{4+\sqrt[4]{3}}$

(b): $\frac{4+\sqrt[3]{3}}{4-\sqrt[3]{3}}$

(c): $\frac{4+\sqrt{3}}{4-\sqrt{3}}$

(d): inget av (a)-(c)

2. Om $a=\frac{1}{3}$, $b=2$ och $x=\frac{{\left(\sqrt{a}+\sqrt{b}\right)}^3-{\left(\sqrt{a}-\sqrt{b}\right)}^3}{ab}$, så gäller att x är lika med:

(a): $3\sqrt{6}$

(b): $6\sqrt{2}$

(c): $3\sqrt{6}+6\sqrt{2}$

(d): inget av (a)-(c)

Även här underlättar det att förenkla innan värdena sätts in. Kuberna i täljaren kan utvecklas med hjälp av kubregeln (ett specialfall av binomialsatsen). Det går även att multiplicera ihop två av faktorerna med kvadreringsreglerna först, och sedan multiplicera den produkten med den tredje faktorn. Detta tar dock längre tid. 

$$\begin{gathered} x=\frac{{\left(\sqrt{a}+\sqrt{b}\right)}^3-{\left(\sqrt{a}-\sqrt{b}\right)}^3}{ab}=\frac{\left({\sqrt{a}}^3+3a\sqrt{b}+3b\sqrt{a}+{\sqrt{b}}^3\right)-\left({\sqrt{a}}^3-3a\sqrt{b}+3b\sqrt{a}-{\sqrt{b}}^3\right)}{ab}= \\ \frac{6a\sqrt{b}+2{\sqrt{b}}^3}{ab} \end{gathered}$$

Nu har vi ett betydligt mindre uttryck att arbeta med. Insättning av a och b:s värden ger nu att: 

$\frac{6·{\displaystyle \frac{1}{3}}·\sqrt{2}+2{\sqrt{2}}^3}{\frac{1}{3}·2}=\frac{2·\sqrt{2}+4\sqrt{2}}{\frac{2}{3}}=\frac{3}{2}·2\sqrt{2}\left(1+2\right)=9\sqrt{2}$

Svar: (d), inget av (a)-(c)

Tillägg: 10 apr 2023 15:15

Alternativ lösning (credit till Dracaena): 

Här kan konceptet difference of cubes användas. Sambandet lyder: 

$x^3-y^3=(x-y)(x^2+xy+y^2)$

I denna uppgift är $x=\sqrt{a}+\sqrt{b}$ och $y=\sqrt{a}-\sqrt{b}$. Det är viktigt att inte sätta in de numeriska värdena av a och b för tidigt. Så länge vi fortfarande kan förenkla, är det bättre att hålla sig till a och b. Det innebär att de två faktorerna $(x-y)$ samt $(x^2+xy+y^2)$ kan förenklas till: 

$$\begin{gathered} (x-y): \\ \left(\sqrt{a}+\sqrt{b}\right)-\left(\sqrt{a}-\sqrt{b}\right)=2\sqrt{b} \end{gathered}$$

respektive:

$$\begin{gathered} \left(x^2+xy+y^2\right): \\ {\left(\sqrt{a}+\sqrt{b}\right)}^2+\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)+{\left(\sqrt{a}-\sqrt{b}\right)}^2= \\ \left(a+2\sqrt{ab}+b\right)+\left(a-b\right)+\left(a-2\sqrt{ab}+b\right)=3a+b \end{gathered}$$

Allt som allt kan vi därför skriva om x till $x=\frac{2\sqrt{b}\left(3a+b\right)}{ab}$. 

Nu kan vi stoppa in värdena av a och b, och beräkna värdet: 

$x=\frac{2\sqrt{b}\left(3a+b\right)}{ab}=\frac{2\sqrt{2}\left(3·{\displaystyle \frac{1}{3}}+2\right)}{{\displaystyle \frac{1}{3}}·2}=\frac{6\sqrt{2}}{{\displaystyle \raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}=9\sqrt{2}$

Svar: (d), inget av (a)-(c).

3. Om a och b är positiva reella tal och $x=\sqrt{a^2+2ab+b^2}-\sqrt{a^2-2ab+b^2}$ så gäller att x är lika med

(a): 2a

(b): 2b

(c): 2ab

(d): inget av (a)-(c)

En fullständig lösning är följande:

Genom att identifiera att uttrycken under rottecknen är utvecklade kvadrater, kan vi snabbt göra omskrivningen: 

$x=\sqrt{a^2+2ab+b^2}-\sqrt{a^2-2ab+b^2}=\sqrt{{\left(a+b\right)}^2}-\sqrt{{\left(a-b\right)}^2}$

Det gäller att $\sqrt{z^2}=\left|z\right|$, vilket vi kan använda för att göra omskrivningen $x=\left|a+b\right|-\left|a-b\right|$. Nu har vi två intervall, $a\ge b$ och $a<b$. I det första intervallet blir $x=\left(a+b\right)-\left(a-b\right)=2b$. I det andra intervallet blir $x=\left(a+b\right)--(a-b)=2a$. Därför gäller varken svarsalternativ a, b eller c. 

Svar: (d): inget av (a)-(c).

En snabbare metod som kan användas är att pröva med exemplet $a=b$. Då får vi att: 

$$\begin{gathered} x=\sqrt{a^2+2a·a+a^2}-\sqrt{a^2-2a·a+a^2}= \\ \sqrt{4a^2}-\sqrt{0}=\mathbf{\left|}\mathbf{2}\mathit{a}\mathbf{\right|} \end{gathered}$$

vars värde är antingen +2a eller -2a beroende på om a (och därmed b) är positivt eller negativt. 

Svar: (d): inget av (a)-(c).

Uppgifter som liknar denna: 

1. Om a och b är positiva reella tal och $x=\sqrt{a^2-4ab+4b^2}-\left(a+2b\right)$ så gäller att x är lika med

(a): $-4b$

(b): $-2a$

(c): $4b$

(d): inget av (a)-(c)

2. Om a och b är positiva reella tal och $x=\frac{\sqrt{9a^2-18ab+b^2}}{2\left|3a-b\right|}$ så gäller att x är lika med

(a): $-\frac{1}{2}$

(b): $0$

(c): $\frac{1}{2}$

(d): inget av (a)-(c)

4. Om $0<a<1$ och $b>2$ så gäller att

(a): $\frac{1}{a}+\frac{1}{b}>3$

(b): $\frac{1}{a}+\frac{1}{b}>\frac{3}{2}$

(c): $\frac{1}{a}+\frac{1}{b}>1$

(d): inget av (a)-(c)

Det är alltid en bra idé att pröva med några enkla värden, exempelvis $a=0,5$ och $b=4$ lika med 2,25. Detta utesluter alternativ (a). 

Helst vill vi minimera värdet av $\frac{1}{a}+\frac{1}{b}$, eftersom vi letar efter en undre gräns, vilket vi gör genom att maximera nämnarna. a kommer då att bli så nära 1 som möjligt, och b så stort som möjligt. Genom att prova med $a=\frac{10}{11}$ och $b=10$ får vi enkla värden, och detta ger oss: 

$\frac{1}{a}+\frac{1}{b}=\frac{1}{10/11}+\frac{1}{10}=\frac{12}{10}=1,2$

Detta utesluter alternativ (b). 

Frågan är dock om det finns en undre gräns, och i så fall om den gränsen är 1. Här går det att göra en kvalificerad gissning och säga att alternativ (c) är rätt. Detta sparar tid, men vi har inte egentligen bevisat att detta är korrekt. 

En formell beräkning är följande: 

$\underset{a\to 1}{\lim }\left(\underset{b\to \infty }{\lim }\left(\frac{1}{a}+\frac{1}{b}\right)\right)=\underset{\to 1}{\underbrace{\underset{a\to 1}{\lim }\left(\frac{1}{a}\right)}}+\underset{\to 0}{\underbrace{\underset{b\to \infty }{\lim }\left(\frac{1}{b}\right)}}=1+0=1$

Svar: (c), $\frac{1}{a}+\frac{1}{b}>1$

Uppgifter som liknar denna:

1. Om $0<a<1$ och $b>2$, och olikheten $\frac{2}{a}+\frac{1}{2b}>x$ gäller, vilket är det största värdet som x kan anta?

(a): $\frac{3}{2}$

(b): $\frac{5}{3}$

(c): 1

(d): inget av (a)-(c)

2. Om $0<a<1$ och $b>2$ så gäller att

(a): $\frac{2}{a^2}+\frac{1}{3b}>2$

(b): $\frac{2}{a^2}+\frac{1}{3b}>\frac{5}{2}$

(c): $\frac{2}{a^2}+\frac{1}{3b}>3$

(d): inget av (a)-(c)

5. Om $0<a<1$ och $b>2$ så gäller att 

(a): $\frac{1}{a}-\frac{1}{b}>\frac{3}{2}$

(b): $\frac{1}{a}-\frac{1}{b}>1$

(c): $\frac{1}{a}-\frac{1}{b}>\frac{1}{2}$

(d): inget av (a)-(c)

Även här är det lämpligt att prova med några värden till att börja med. Exemplet med $a=\frac{10}{11}$ och $b=10$ i uppgift (5) ger här värdet

$\frac{1}{a}-\frac{1}{b}=\frac{1}{10/11}-\frac{1}{10}=1$

vilket i ett svep utesluter både alternativ (a) och (b). Frågan är då om (c) eller (d) är rätt. 

För att minimera värdet i vänsterledet, behöver vi minimera $\frac{1}{a}$ och maximera $\frac{1}{b}$. Detta gör vi genom att låta a gå mot 1, och b gå mot 2. Detta ger oss gränsvärdet: 

$\underset{a\to 1}{\lim }\left(\frac{1}{a}\right)-\underset{b\to 2}{\lim }\left(\frac{1}{b}\right)=1-\frac{1}{2}=\frac{1}{2}$

Svar: (c), $\frac{1}{a}-\frac{1}{b}>\frac{1}{2}$

Uppgifter som liknar denna:

1. Om $0<a<1$ och $b>2$ så gäller att

(a): $\frac{1}{a}-\frac{2}{b^2}>\frac{1}{2}$

(b): $\frac{1}{a}-\frac{2}{b^2}>1$

(c): $\frac{1}{a}-\frac{2}{b^2}>\frac{3}{2}$

(d): inget av (a)-(c)

2. Om $0<a<1$och $b>2$, och olikheten $\frac{1}{b^2}-\frac{3}{a}>x$ gäller, vilket är det största värdet som x kan anta?

(a): 0

(b): $\frac{1}{2}$

(c): 1

(d): inget av (a)-(c)

6. Om $x⊞y=x^2+xy+y^2$ för alla reella tal x och y, och de reella talen a och b är sådana att $a⊞b>0$, så kan man dra slutsatsen att

(a): $a^2+b^2\neq0$

(b): $a>0$ och $b>0$

(c): $a+b\neq0$

(d): inget av (a)-(c) behöver gälla

Det kan vara lättare att tänka på x⊞y = $x^2+xy+y^2$ som funktionen $f(x,y)=x^2+xy+y^2$. 

Vi har fått informationen att $a⊞b>0$, dvs. att $a^2+ab+b^2>0$. Frågan är nu om detta medför att något av svarsalternativen måste vara sant. Vi kan testa detta genom att testa om det går att bryta mot påståendet i respektive svarsalternativ, medan kravet att $a^2+ab+b^2>0$ fortfarande är uppfyllt. 

(b): Kan vi säkert säga att både a och b ska vara större än noll? Vad händer om a är 1 och b är noll? Då får vi att $1^2+1·0+0^2$, vilket är större än noll. Vi kan därför inte säkert säga att a och b båda är större än noll, och det går därför inte att säga att $a>0$ och $b>0$. 

(c): Kan vi säkert säga att $a+b\neq0$? Detta villkor är inte sant om $a=-b$. Vi undersöker den situationen. Olikheten som måste gälla är att $a^2+ab+b^2>0$. När $a=-b$ blir denna olikhet: 

$a^2+ab+b^2={(-b)}^2+(-b)b+b^2=2b^2-b^2={\mathit{b}}^{\mathbf{2}}$

Eftersom a och b är reella, är $b^2$ större än eller lika med noll för alla värden på b. Frågan är då om b kan vara noll. Om b får vara noll, faller olikheten $b^2>0$. 

Om b är noll, måste även a vara noll, eftersom vi undersöker situationen $a=-b$. Om både a och b är noll, uppfylls inte olikheten $a^2+ab+b^2>0$, som uppgiften kräver. Det betyder att b inte kan vara noll. Vi kan då säkert dra slutsatsen att $b^2>0$, och därmed kan värden på a och b sådana att $a=-b$ uppfylla uppgiftens krav. Det går alltså inte att säga att $a+b=0$. 

(a): Kan det vara så att $a^2+b^2=0$? Det kan skrivas om till $a^2=-b^2$. För reella tal är den likheten endast uppfylld för $a=b=0$. Uppgiften kräver att uttrycket $a^2+ab+b^2$ ska vara större än noll. Men om både a och b är noll, är den olikheten inte uppfylld. Det finns alltså inga tal a och b sådana att $a^2+b^2=0$, som också uppfyller att $a^2+ab+b^2>0$. Vi kan därför vara säkra på att det kravet gäller. 

Svar: (a), $a^2+b^2\neq0$.

Uppgifter som liknar denna: 

1. Om $x△y=\frac{x}{y^2}+\frac{y}{x^2}$ för alla reella tal x och y, och de reella talen a och b uppfyller att $a△b$ är jämnt, så kan man dra slutsatsen att

(a): $\left(-x\right)△y=x△(-y)$

(b): $-\left(x△y\right)=\left(-x\right)△\left(-y\right)$

(c): $x^2△y^2$

(d): inget av (a)-(c) behöver gälla

2. Om $x\diamond y=\frac{1}{x^2-y^2}$ för alla reella tal x och y, och de reella talen a och b uppfyller att $a\diamond b>0$, då kan man dra slutsatsen att

(a): $a+b>0$

(b): $a>b$

(c): $\frac{1}{a+b}>0$

(d): inget av (a)-(c) behöver gälla

7. Talet x är sådant att $x^2>x$. Man kan då dra slutsatsen att

(a): $x<0$

(b): $x>1$

(c): $x<0$ eller $x>1$

(d) inget av (a)-(c)

Denna uppgift går att lösa genom faktorisering, eller genom att prova med olika tal. 

Faktorisering: 

$x^2>x$ kan skrivas om till $x^2-x>0$, som kan faktoriseras till $x(x-1)>0$. Om x är mellan noll och ett, är x positivt, men $(x-1)$ negativt, vilket ger en negativ produkt, och då är olikheten inte uppfylld. Men om x är mindre än noll, eller större än ett är olikheten uppfylld, vilket ger oss svaret (c), $x<>$ eller $x>1$. 

Pröva med olika tal: 

Testa likheten med: 

• Stora och små negativa tal
• Noll
• Stora och små positiva tal

• Stora och små negativa tal:
  Om $x=-10$, får vi olikheten $(-10)^2=100>-10$, vilket stämmer. 
  Om $x=-0,1$ får vi olikheten $(-0,1)^2=0,01>-0,1$, vilket stämmer. 
• Noll: 
  Om $x=0$ får vi olikheten $0^2=0>0$, vilket inte stämmer. 
• Stora och små positiva tal: 
  Om $x=10$ får vi olikheten $10^2=100>10$, vilket stämmer. 
  Om $x=0,1$ får vi olikheten $0,1^2=0,01>0,1$, vilket inte stämmer. 

För negativa tal, samt för lite större positiva tal är olikheten uppfylld, men inte för små. Hur är det med 0,5? 1? 1,5? 

$0,5^2=0,25>0,5$ stämmer inte. 

$1^2=1>1$ stämmer inte.

$1,5^2=2,25>1,5$ den olikheten stämmer. 

Det verkar alltså som att gränsen för positiva tal går vid 1. 

Svar: (c), $x<0$ eller $x>1$

Uppgifter som liknar denna: 

1. Talet x är sådant att $2x^2>-x$. Man kan då dra slutsatsen att

(a): $x<-\frac{1}{2}$ och $x>0$

(b): $0<x<\frac{1}{\sqrt{2}}$

(c): $x>\frac{1}{2}$

(d): inget av (a)-(c)

2. Talet x är sådant att $x^3>4x$. Man kan då dra slutsatsen att

(a): $0<x<2$ och $x<-2$

(b): $-2<x<0$

(c): $-2<x<0$ och $x>2$

(d): inget av (a)-(c)

8. Antalet heltalslösningar till olikheten $\frac{1}{x}>\frac{1}{x-4}$ är

(a): 0

(b): 4

(c): 5

(d): inget av (a)-(c)

Här kan man antingen pröva sig fram eller lösa olikheten algebraiskt. Det går även att rita, för den som känner sig bekväm med det. 

Pröva sig fram: 

Om x är negativt, säg -2, får vi följande olikhet: $\frac{1}{-2}>\frac{1}{-2-4} \iff -\frac{1}{2}>-\frac{1}{6}$, vilket inte är sant. $x>x-4$ för alla negativa tal, vilket medför att $\frac{1}{x}$ är mindre än $\frac{1}{x-4}$ för alla negativa tal. I intervallet $x<>$ finns inga lösningar att hitta, med andra ord. 

Om x är noll är vänsterledet odefinierat, och det kan därför inte vara en lösning. Hur är det med små positiva heltal som 1 och 2? 

$$\begin{gathered} x=1: \frac{1}{1}>\frac{1}{1-4}\iff 1>-\frac{1}{3} \\ x=2: \frac{1}{2}>\frac{1}{2-4}\iff 0,5>-0,5 \end{gathered}$$

Båda stämmer. $x=3$ ger olikheten $\frac{1}{3}>-1$, vilket också stämmer. För $x=4$ är högerledet inte definierat. 

Håller olikheten för $x=5$? 

$\frac{1}{5}>\frac{1}{5-4}\iff \frac{1}{5}>1$ 

Nej. Inte heller större värden på x, såsom $x=10$ eller $x=100$ fungerar. Det verkar med med andra ord finnas tre lösningar.

Svar: (d), inget av (a)-(c).

Algebraisk lösning: 

Det går att multiplicera båda led med x och sedan $x-4$, men eftersom vi har en olikhet måste vi då ta stor hänsyn till vilket tecken x har. Ett enklare sätt är att skriva båda bråk på samma bråkstreck: 

$$\begin{gathered} \frac{1}{x}-\frac{1}{x-4}>0 \\ \frac{(x-4)-x}{x(x-4)}>0 \\ \frac{-4}{x(x-4)}>0 \end{gathered}$$

Denna olikhet är sann endast om nämnaren är negativ. Det går att göra en teckentabell, men för att spara tid kan vi konstatera att både x och $x-4$ måste ha olika tecken, vilket de har endast om x ligger i intervallet 0 till 4. Om x är noll eller fyra är bråket odefinierat (nämnaren blir noll), vilket ger totalt tre heltalslösningar: 1, 2 och 3. 

Svar: (d), inget av (a) till (c). 

Rita: 

Här är det en stor fördel att använda rutigt papper, för att få till raka och jämna koordinataxlar. Det går självklart att rita med en linjal också, men det tar längre tid och risken för fel ökar. 

En skiss av de två funktionerna $f\left(x\right)=\frac{1}{x}$ och $g\left(x\right)=\frac{1}{x-4}$ ser ut ungefär som nedan. Vi letar efter de områden där $f\left(x\right)>g\left(x\right)$. 

(g(x) är endast f(x) fast förskjuten fyra steg åt höger i x-led)

Endast i den gröna rutan ligger f(x) över g(x). I intervallet finns tre heltalsvärden som uppfyller olikheten. 

Svar: (d), inget av (a) till (c). 

Uppgifter som liknar denna: 

1. Antalet negativa heltalslösningar till olikheten $\frac{5}{2x-4}\ge \frac{1}{4+x}$ är: 

(a): 3

(b): 4

(c): 5

(d): inget av (a)-(c)

2. Antalet heltalslösningar till olikheten $\frac{2}{x-2}<\frac{x}{-2+x}$ är

(a): 0 

(b): 4

(c): 10

(d): inget av (a)-(c)

9. Givet är ekvationen $2x^2+x+p=0$, där p är ett negativt tal. För ekvationen gäller då att

(a): den har två olika icke-reella lösningar

(b): den har två reella lösningar med olika tecken

(c): den har två reella lösningar med samma tecken

(d): inget av (a)-(c) behöver gälla generellt

Denna uppgift kan lösas grafiskt, eller algebraiskt. 

Grafisk lösning: Rita upp grafen till $f(x)=2x^2+x$. Den har sin minimipunkt i origo. Grafen till $f(x)+p$ är då f(x) men förskjuten i y-led. Eftersom p är negativt, hamnar minimipunkten under x-axeln, i punkten $(0,p)$. Det innebär att den ena sidan av grafen kommer att skära x-axeln då $x>0$ och den andra sidan av grafen kommer att skära x-axeln då $x<>$. Det måste därför finnas två reella lösningar med olika tecken.

Algebraisk lösning: Hur många och vilka lösningar har ekvationen $2x^2+x+p=0$, för $p<>$? 

För att kunna använda PQ-formeln behöver vi en ekvation på formen $x^2+px+q=0$:

$$\begin{gathered} 2x^2+x+p=0 \\ {x}^2+\frac{x}{2}+\frac{p}{2}=0 \end{gathered}$$

PQ-formeln ger nu att: 

$$\begin{gathered} x=-\frac{1}{4}\pm \sqrt{{\left(-\frac{1}{4}\right)}^2-\frac{p}{2}}= \\ x=-\frac{1}{4}\pm \sqrt{\frac{1}{16}-\frac{p}{2}}=-\frac{1}{4}\pm \sqrt{\frac{1-8p}{16}} \end{gathered}$$

Eftersom p är ett negativt tal kommer ekvationen att ha reella lösningar för alla p. När p är ett större negativt tal, blir skillnaden mellan de två lösningarna större. Om $p\rightarrow0^+$ kommer värdet på x att gå mot:

$$\begin{gathered} x=\underset{p\to 0^{+}}{\lim }\left(-\frac{1}{4}\pm \sqrt{\frac{1-8p}{16}}\right)=-\frac{1}{4}\pm \frac{1}{4} \\ {x}_1=0; x_2=-\frac{1}{2} \end{gathered}$$

Men eftersom $p>0$ kommer alla lösningar att vara reella och ha olika tecken.

Svar: (b), den har två reella lösningar med olika tecken.

Uppgifter som liknar denna: 

Vilket av följande alternativ gäller för respektive ekvation nedan? 

(a): den har två olika icke-reella lösningar

(b): den har två reella lösningar med olika tecken

(c): den har två reella lösningar med samma tecken

(d): inget av (a)-(c) behöver gälla generellt

1. $p{x}^2-10px+25p+1=0$, $p<>$.

2. $p{x}^2+8x-4+p=0$, $p>0$.

3. $4x^2+3x-p=1$, p är ett positivt tal

10. Antalet lösningar till ekvationen $\left|\sin \left(\frac{x}{2}\right)\right|=1$ i intervallet $(-2\mathrm{\pi }, \mathrm{\pi })$ är: 

(a): 1

(b): 2

(c): 3

(d): inget av (a) till (c)

Här är den kanske enklaste metoden att rita. Börja med rita upp grafen till $f\left(x\right)=\sin \left(\frac{x}{2}\right)$: 

Absolutbeloppet innebär att alla negativa värden speglas i x-axeln, vilket ger nedanstående skiss: 

Var skär den grafen linjen $y=1$? I vår skiss ser vi att skärningspunkterna är:

Två skärningspunkter. Men! Det är ett öppet intervall $\left(-2\mathrm{\pi },\mathrm{\pi }\right)$, vilket innebär att endast $x=-\mathrm{\pi }$ är en godtagbar lösning. 

Svar: (a), 1.

Uppgifter som liknar denna: 

1. Antalet lösningar till ekvationen $\left|\cos \left(\frac{x}{4}\right)\right|=\frac{1}{2}$ i intervallet $\left(-3\mathrm{\pi }, 2\mathrm{\pi }\right)$:

(a): 2

(b): 3

(c): 4

(d): inget av (a)-(c)

2. Antalet lösningar till ekvationen $\left|\tan \left(\frac{x-{\displaystyle \raisebox{1ex}{$\mathrm{\pi }$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{2}\right)\right|=1$ i intervallet $\left(-\mathrm{\pi }, 2\mathrm{\pi }\right)$:

(a): 0

(b): 1

(c): 2

(d): inget av (a)-(c)

3. Antalet lösningar till ekvationen $\left|\sin \left(x\right)\right|=\left|\frac{x}{2}\right|$ i intervallet $\left[-\mathrm{\pi }, 2\mathrm{\pi }\right]$:

(a): 2

(b): 3

(c): 4

(d): inget av (a)-(c)

11. Summan $S=1+\frac{1}{2}+\frac{1}{4}+...+\frac{1}{2^{2022}}$ är lika med 

(a): $2\left(2^{2022}-1\right)$

(b): $\frac{2^{2022}-1}{2}$

(c): $\frac{2^{2022}-1}{2^{2021}}$

(d): inget av (a) till (c)

Detta är en geometrisk summa, som kan skrivas om till $S=\frac{1}{2^0}+\frac{1}{2^1}+\frac{1}{2^2}+...+\frac{1}{2^{2022}}$. 

Det kan vara värt att notera att summan verkar gå mot 2, kanske 3 – ett ganska litet tal i alla fall. Både alternativ (a) och (b) utgör enormt stora tal (över 2²⁰⁰⁰), och kan därför uteslutas direkt. 

En geometrisk summa på formen $a+ak+a{k}^2+...+a{k}^n$ har summan $S=\frac{a\left(k^{n+1}-1\right)}{k-1}$. I vårt fall är $a=1$ och $k=\frac{1}{2}$, vilket ger summan: 

$S=\frac{{\left({\displaystyle \frac{1}{2}}\right)}^{2022+1}-1}{{\displaystyle \frac{1}{2}}-1}=-2\left({\left(\frac{1}{2}\right)}^{2023}-1\right)=2-{\left(\frac{1}{2}\right)}^{2022}\underset{\mathrm{även}}{=}\frac{2^{2023}-1}{2^{2022}}$

Detta uttryck stämmer inte med något av svarsalternativen, och framförallt inte med det enda alternativ vi inte redan uteslutit. Därför blir svaret (d), inget av (a)-(c). 

Svar: (d), inget av (a) till (c).

Uppgifter som liknar denna: 

1. Summan $2+\frac{4}{3}+\frac{8}{9}+...+\frac{2^{2001}}{3^{2000}}$ är lika med

(a): $6-\frac{2^{2002}}{3^{2001}}$

(b): $6-\frac{2^{2001}}{3^{2000}}$

(c): $6-\frac{2^{2002}}{3^{2000}}$

(d): inget av (a)-(c)

2. Summan $\frac{1}{64}+\frac{1}{256}+...+\frac{1}{4^{100}}$ är lika med

(a): $\frac{4}{3}-\frac{1}{3·4^{100}}-\frac{21}{16}$

(b): $\frac{4^{101}-1}{3·4^{100}}$

(c): $\frac{4}{3}-\frac{21}{16}$

(d): inget av (a)-(c)

12. För alla positiva reella tal $x,y$ gäller att 

(a): $\sqrt{x+y}=\sqrt{x}+\sqrt{y}$

(b): $\sqrt{xy}=\sqrt{x}·\sqrt{y}$

(c): $\sqrt{x+y}=\sqrt{x}·\sqrt{y}$

(d): inget av (a)-(c) gäller generellt

Potenslagarna säger att $a^c·b^c={\left(ab\right)}^c$ (för positiva, reella tal). Detta gäller även för rötter (a:te roten ur är en potens med exponenten $\frac{1}{a}$). Därför är alternativ (b) korrekt. 

Det går även bra att prova några tal, för att utesluta felaktiga alternativ. Det kan vara hjälpsamt att testa med kvadrattal, för att inte behöva räkna med krångliga rötter, men det är inte strikt nödvändigt. 

$x=1,\;y=4$: 

(a): 

$$\begin{gathered} \sqrt{1+4}=\sqrt{1}+\sqrt{4} \\ \sqrt{5}=1+2 \\ \sqrt{5}\ne 3 \end{gathered}$$

(a) kan uteslutas. 

(b): 

$$\begin{gathered} \sqrt{1·4}=\sqrt{1}·\sqrt{4} \\ \sqrt{4}=1·2 \\ 2=2 \end{gathered}$$

(korrekt)

(c): 

$$\begin{gathered} \sqrt{1+4}=\sqrt{1}·\sqrt{4} \\ \sqrt{5}=1·2 \\ \sqrt{5}\ne 2 \end{gathered}$$

(c) kan uteslutas.

Självklart är detta inget bevis, och det skulle absolut kunna vara en slump att (b) stämmer för just dessa värden, men för den som känner sig osäker på potenslagarna, kan det vara värt att utesluta alternativ. 

(b), $\sqrt{xy}=\sqrt{x}·\sqrt{y}$. 

Uppgifter som liknar denna: 

1. För alla positiva reella tal a, b och c gäller att 

(a): $a^{b+c}=a^{b^c}$

(b): $a^{b^c}=a^{c^b}$

(c): $a^{b^c}=a^{b·c}$

(d): inget av (a)-(c) gäller generellt

2. För alla positiva reella tal a, b och c gäller att 

(a): $a^c·b^c={\left(a+b\right)}^c$

(b): $a^c·b^c={\left(a·b\right)}^c$

(c): $a^c·b^c={\left(a^c+b^c\right)}^c$

(d): inget av (a)-(c) gäller generellt

13. För alla positiva reella tal $x,y$ gäller att

(a): $\ln (x+y)=\ln \left(x\right)+\ln \left(y\right)$

(b): $\ln \left(xy\right)=\ln \left(x\right)·\ln \left(y\right)$

(c): $\ln (x+y)=\ln \left(x\right)·\ln \left(y\right)$

(d): inget av (a)-(c) gäller generellt

Här hjälper kunskap om logaritmlagarna. Den logaritmlag som är närmast de likheter som finns som alternativ är $\ln \left(xy\right)=\ln \left(x\right)+\ln \left(y\right)$, men någon sådan ekvation saknas bland alternativen. Därför blir svaret (d), inget av (a)-(c) gäller generellt. 

Det kan även hjälpa att prova sig fram. Det hjälper då att välja tal som är lätta att logaritmera, exempelvis potenser av e. 

Exemplet $x=1,\;y=e^3$ ger följande resultat: 

(a): 

$$\begin{gathered} \ln \left(1+e^3\right)\stackrel{?}{=}\underset{0}{\underbrace{\ln \left(1\right)}}+\ln \left(e^3\right) \\ \ln (1+e^3)\ne 0+\ln \left(e^3\right) \end{gathered}$$

(b): 

$\ln (1·e^3)\stackrel{?}{=}\ln \left(1\right)·\ln \left(e^3\right)$

ln(1) är noll, och ln(e³) är 3. Det ger oss

$3=0·3$

vilket inte är sant.

(c): 

$\ln (1+e^3)\stackrel{?}{=}\ln \left(1\right)·\ln \left(e^3\right)$

Även här får vi att ln(1) är noll, och ln(e³) är 3, vilket ger

$$\begin{gathered} \ln (1+e^3)\stackrel{?}{=}0·3 \\ \ln (1+e^3)\ne 0 \end{gathered}$$

Inget av alternativen fungerar för vårt exempel. Vi kan därför konstatera att svaret är (d). 

Svar: (d), inget av (a)-(c)

Uppgifter som liknar denna: 

1. För alla positiva reella tal x och y gäller att 

(a): $\ln \left(\frac{a}{b}\right)=\ln \left(a-b\right)$

(b): $\ln \left(a-b\right)=\frac{a}{b}$

(c): $\ln \left(\frac{a}{b}\right)=\ln \left(a\right)-\ln \left(b\right)$

(d): inget av (a)-(c) gäller generellt

2. För alla positiva reella tal x och y gäller att 

(a): $\ln \left(a^b\right)=\ln \left(a\right)·\ln \left(b\right)$

(b): $\ln \left(a^b\right)=b·\ln \left(a\right)$

(c): $\ln \left(a^b\right)=a·\ln \left(b\right)$

(d): inget av (a)-(c) gäller generellt

14. Om $\sin \left(\alpha \right)=p$ och $\mathrm{\pi }<\alpha \mathit{<}2\mathrm{\pi }$ så gäller att $\left|\cos \left(\alpha \right)\right|$ är lika med

(a): $\sqrt{1-p^2}$

(b): $-\sqrt{1-p^2}$

(c): $\pm \sqrt{1-p^2}$

(d): inget av (a)-(c)

Vinkeln alfa ligger på enhetscirkeln i den tredje eller fjärde kvadranten:

Trigonometriska ettan gör att vi kan hitta ett värde på cosinus: 

$$\begin{gathered} \underset{p^2}{\underbrace{{\sin }^2\alpha }}+{\cos }^2\alpha =1 \\ \cos \left(\alpha \right)=\underset{?}{\overline{)\pm }}\sqrt{1-p^2} \end{gathered}$$

Beroende på vilken kvadrant vinkeln alfa ligger i, kommer tecknet framför rotuttrycket att bli positivt eller negativt. Men eftersom värdet av $\left|\cos \left(\alpha \right)\right|$ söks, söker vi värdet av $\left|\underset{?}{\overline{)\pm }}\sqrt{1-p^2}\right|$, så oavsett vilket tecken $\cos{(\alpha)}$ har, kommer värdet av $|\cos{(\alpha)}|$ att vara positivt. 

Värdet av $\sqrt{1-p^2}$ är alltid positivt eller eller noll. Vi kan därför säkert säga att $\left|\cos \left(\alpha \right)\right|=\sqrt{1-p^2}$. 

Svar: (a), $\sqrt{1-p^2}$. 

Tillägg: 1 maj 2023 17:58

Uppgifter som liknar denna: 

1. Om $\cos \left(x\right)=\frac{1}{p}$ och $\frac{\mathrm{\pi }}{2}<x<\frac{3\mathrm{\pi }}{2}$ så gäller att $-\sin \left(x\right)$ är lika med

(a): $-\frac{\sqrt{p^2-1}}{p}$

(b): $\frac{\sqrt{p^2-1}}{p}$

(c): $\frac{\sqrt{p^2-1}}{\left|p\right|}$

(d): inget av (a)-(c)

2. Om $\sin \left(2x\right)=p$ och $-\frac{\mathrm{\pi }}{4}<x<\frac{\mathrm{\pi }}{4}$ så gäller att $\left|-\cos \left(2x\right)\right|$ är lika med

(a): $\sqrt{1-p^2}$

(b): $\pm \sqrt{1-p^2}$

(c): $-\sqrt{1-p^2}$

(d): inget av (a)-(c)

3. Om $\sin \left(2x\right)=-\frac{3}{2}$ och $\frac{3\mathrm{\pi }}{2}<x<2\mathrm{\pi }$ så gäller att $\left|-\tan \left(x\right)\right|$ är lika med

(a): $\frac{3}{\sqrt{7}}$

(b): $-\frac{3}{\sqrt{7}}$

(c): $\pm \frac{3}{\sqrt{7}}$

(d): inget av (a)-(c)

15. Om $\sin \left(\alpha \right)=p$ och $\mathrm{\pi }<\alpha <2\mathrm{\pi }$ så gäller att $\left|\tan \left(\alpha \right)\right|$ är lika med

(a): $\frac{p}{\sqrt{1-p^2}}$

(b): $-\frac{p}{\sqrt{1-p^2}}$

(c): $\pm \frac{p}{\sqrt{1-p^2}}$

(d): inget av (a)-(c)

Även i denna uppgift ligger vinkeln i tredje eller fjärde kvadranten: 

För tangensfunktioner gäller likheten $\tan \left(x\right)=\frac{\sin \left(x\right)}{\cos \left(x\right)}$. Täljaren har vi fått i uppgiften, och nämnaren kan vi beräkna med trigonometriska ettan: 

$$\begin{gathered} 1={\sin }^2\left(x\right)+{\cos }^2\left(x\right) \\ 1=p^2+{\cos }^2\left(\alpha \right) \\ \cos \left(\alpha \right)=\underset{\mathrm{tecken}?}{\underbrace{\overline{)\pm }}}\sqrt{1-p^2} \end{gathered}$$

I dessa uppgifter är det viktigt att hålla isär ett tals tecken och talets storlek/värde. Vilket tecken värdet av $\cos \left(\alpha \right)$ har varierar beroende på hur stor vinkeln är, men storleken är $\sqrt{1-p^2}$. Men eftersom vi söker just $\left|\tan \left(\alpha \right)\right|$, behöver vi titta noggrannare på täljarens och nämnarens tecken. Något som kan underlätta är att notera att $\left|\frac{a}{b}\right|=\frac{\left|a\right|}{\left|b\right|}$. Det innebär att $\left|\tan \left(x\right)\right|=\left|\frac{\sin \left(x\right)}{\cos \left(x\right)}\right|=\frac{\left|\sin \left(x\right)\right|}{\left|\cos \left(x\right)\right|}$. 

• $\sin \left(x\right)=p$ är negativ i hela intervallet. Absolutbeloppet av $\sin{(x)}$ kan därför skrivas som $-p$. 
• $\cos \left(x\right)=\underset{\mathrm{tecken}?}{\underbrace{\pm }}\sqrt{1-p^2}$ har ett tecken som varierar beroende på intervallet. Viktigt att notera är dock att $\sqrt a\geq0$ för alla reella a. Det innebär att $\left|\pm \sqrt{1-p^2}\right|=\sqrt{1-p^2}$, oavsett vilket tecken som gäller för en viss vinkel i intervallet.

Detta kan vi nu sätta ihop: 

$\left|\tan \left(x\right)\right|=\left|\frac{\sin \left(x\right)}{\cos \left(x\right)}\right|=\frac{\left|\sin \left(x\right)\right|}{\left|\cos \left(x\right)\right|}=\frac{-p}{\sqrt{1-p^2}}=-\frac{p}{\sqrt{1-p^2}}$

Svar: (b), $-\frac{p}{\sqrt{1-p^2}}$.

Tillägg: 1 maj 2023 20:35

Uppgifter som liknar denna: 

1. Om $\sin \left(x\right)=2p$ och $\frac{\mathrm{\pi }}{2}<x<\frac{3\mathrm{\pi }}{2}$ så gäller att $-\tan \left(x\right)$ är lika med

(a): $-\frac{2p}{\sqrt{1-4p^2}}$

(b): $\frac{2p}{\sqrt{1-4p^2}}$

(c): $\pm \frac{2p}{\sqrt{1-4p^2}}$

(d): inget av (a)-(c)

2. Om $\sin \left(x\right)=q$ och $0<x<\mathrm{\pi }$ så gäller att $-\tan \left(x\right)$ är lika med

(a): $\frac{q}{\sqrt{1-q^2}}$

(b): $-\frac{q}{\sqrt{1-q^2}}$

(c): $\pm \frac{q}{\sqrt{1-q^2}}$

(d): inget av (a)-(c)

16. För alla reella $x,y$ gäller att 

(a): $\cos \left(x\right)+\cos \left(y\right)=2\sin \left(\frac{x+y}{2}\right)\sin \left(\frac{x-y}{2}\right)$

(b): $\cos \left(x\right)+\cos \left(y\right)=2\sin \left(\frac{x+y}{2}\right)\cos \left(\frac{x-y}{2}\right)$

(c): $\cos \left(x\right)+\cos \left(y\right)=2\sin \left(\frac{x-y}{2}\right)\cos \left(\frac{x+y}{2}\right)$

(d): $\cos \left(x\right)+\cos \left(y\right)=2\cos \left(\frac{x+y}{2}\right)\cos \left(\frac{x-y}{2}\right)$

Här är det lätt att börja försöka förenkla med additions- och subtraktionsformlerna för sinus och cosinus, och även om det inte är fel, är det en omväg. Det snabbaste sättet är troligtvis att testa med några enkla tal, exempelvis $x=y=0$. Då får vi att vänsterledet i alla svarsalternativ ska vara lika med 2. Det vi kan notera är dock att $\frac{x-y}{2}=\frac{x+y}{2}=0$, och $\sin{(0)}=0$. För våra olika svarsalternativ får vi därför: 

(a): $2=2·0·0$ [stämmer ej]

(b): $2=2·0·1$ [stämmer ej]

(c): $2=2·0·1$ [stämmer ej]

(d): $2=2·1·1$ [korrekt]

Genom att utnyttja att sin(0) = 0, har vi nu med ett enda exempel uteslutit alla svar utom ett. 

Svar: (d), $\cos \left(x\right)+\cos \left(y\right)=2\cos \left(\frac{x+y}{2}\right)\cos \left(\frac{x-y}{2}\right)$

Uppgifter som liknar denna: 

1. För alla reella $x,y$ gäller att 

(a): $\cos \left(\frac{x}{2}\right)=\sqrt{\frac{1+\cos \left(x\right)}{2}}$

(b): $\cos \left(\frac{x}{2}\right)=\sqrt{\frac{1-\cos \left(x\right)}{2}}$

(c): $\cos \left(\frac{x}{2}\right)=\sqrt{\frac{1+\sin \left(x\right)}{2}}$

(d): inget av (a)-(c) 

2. För alla reella $x,y$ gäller att 

(a): $\tan \left(2x\right)=\frac{2\tan \left(x\right)}{1-{\tan }^2\left(x\right)}$

(b): $\tan \left(2x\right)=\frac{2\tan \left(x\right)}{1+{\tan }^2\left(x\right)}$

(c): $\tan \left(2x\right)=\frac{1-{\tan }^2\left(x\right)}{2\tan \left(x\right)}$

(d): $\tan \left(2x\right)=\frac{1+{\tan }^2\left(x\right)}{2·\tan \left(x\right)}$

3. För alla reella $x,y$ gäller att:

(a): $\tan \left(x+y\right)=\frac{\tan \left(x\right)-\tan \left(y\right)}{1-\tan \left(x\right)\tan \left(y\right)}$

(b): $\tan \left(x+y\right)=\frac{\tan \left(x\right)+\tan \left(y\right)}{1-\tan \left(x\right)\tan \left(y\right)}$

(c): $\tan \left(x+y\right)=\frac{\tan \left(x\right)+\tan \left(y\right)}{1+\tan \left(x\right)\tan \left(y\right)}$

(d): $\tan \left(x+y\right)=\frac{\tan \left(x\right)-\tan \left(y\right)}{1-\tan \left(x\right)\tan \left(y\right)}$

17. Sträckan CP är höjd i triangeln ABC och punkten P ligger på sidan AB. Man kan då dra slutsatsen att

(a): sträckan CP delar vinkeln vid C i två lika delar

(b): $\left|AP\right|=\left|BP\right|$

(c): vinkeln vid C är trubbig

(d): inget av (a)-(c)

Här är det lättast att rita upp en eller några olika trianglar som uppfyller uppgiftens villkor, och undersöka om de olika svarsalternativen stämmer. Ett exempel är denna: 

Vilka svarsalternativ stämmer för denna triangel? 

(a): Nej, sträckan CP delar inte vinkeln vid C i två lika delar.

(b): Nej, sträckorna $\left|AP\right|$ och $\left|BP\right|$ är inte lika långa.

(c): Nej, vinkeln vid C är inte trubbig.

Vi har alltså hittat trianglar som motsäger svarsalternativ (a), (b) och (c).

Svar: (d), inget av (a)-(c).

Uppgifter som liknar denna: 

1. I triangeln ABC utgör sträckan BP en höjd i triangeln, och BP är dessutom en bisektris till vinken i hörnet B. Då gäller att

(a): Vinkeln i hörnet B är spetsig.

(b): Triangeln ABC är liksidig.

(c): $\left|AP\right|=\left|PC\right|$

(d): Inget av (a)-(c)

2. I fyrhörningen ABCD finns triangeln ABD. Sträckan AP är en höjd i triangeln, och punkten P ligger på sidan BD. Då gäller att

(a): Förlängningen av höjden AP skär punkten C.

(b): $\left|BP\right|=\left|DP\right|$

(c): Diagonalerna AC och BD skär varandra i en rät vinkel.

(d): Inget av (a)-(c).

18. Två av höjderna i en triangel skär varandra och den spetsiga vinkeln mellan dem är 45°. Då gäller att

(a) en av triangelns vinklar är 45°

(b) en av triangelns vinklar är 135°

(c) det går inte att avgöra

(d) det fi􏰁nns ingen sådan triangel

Här behöver vi först (försöka) konstruera den/de trianglar som uppgiften pratar om. Börja med den information som getts i uppgiften: 

1. Två höjder skär varandra sådant att den spetsiga vinkeln mellan dem är 45°: 

Nu kan vi rita in de sidor som dessa höjder tillhör (höjder är alltid vinkelräta mot sina sidor): 

Den tredje sidan kan skära de heldragna linjerna lite hursomhelst, så vi får fokusera på den vinkel som bildats av de linjer vi känner till (vinkeln EGF). Vinkeln EHF är $180°-45°=135°$, och vinklarna HEG samt GFH är räta (då de bildats av sidorna och deras vinkelräta höjder). Med en fyrhörnings vinkelsumma på 360° måste vinkeln FGE, som utgör en av triangelns tre hörn, vara 45°. 

Svar: (a), en av triangelns vinklar är 45°.

Uppgifter som liknar denna: 

1. I triangeln ABC finns tre höjder. Höjderna eller deras förlängningar skär varandra varken innanför eller utanför ABC. Då gäller att

(a): triangeln ABC är spetsig

(b): triangeln ABC är rät

(c): triangeln ABC är trubbig

(d): det finns ingen sådan triangel

2. I triangeln ABC finns tre höjder som skär varandra på så sätt att en mindre triangel, DEF, bildas inuti ABC. Då gäller att

(a): Triangeln ABC är spetsig

(b): Triangeln ABC är rät

(c): Triangeln ABC är trubbig

(d): det finns ingen sådan triangel

19. Två av höjderna i en triangel skär inte varandra och den spetsiga vinkeln mellan deras förlängningar är 45°. Då gäller att

(a): en av triangelns vinklar är 45°

(b): en av triangelns vinklar är 135°

(c): det går inte att avgöra

(d): det fi􏰁nns ingen sådan triangel

För att en triangels höjder ska skära utanför triangeln måste triangeln vara trubbig. I denna uppgift är villkoret att två av höjderna skär varandra i en vinkel som är 45° stor. Vi får då två möjligheter. Antingen är det två intilliggande höjder som skär varandra i en 45° vinkel, eller är det de två höjder som inte ligger intill varandra som utgör den 45°-vinkeln. Skissa två trianglar som (ungefär) uppfyller respektive möjlighet: 

Närliggande höjder skär i 45° vinkel:

De två höjder som inte ligger intill varandra skär i 45° vinkel: 

Dessa bilder är exakta, men under provet räcker det med ungefärliga skisser. Tydligt är att det helt klart finns sådana trianglar, vilket utesluter alternativ (d). 

Den som känner sig säker nog på sina skisser kan redan här konstatera att vi har två helt olika trianglar, som inte har någon vinkel gemensamt, och att det därför inte går att säga något om hur stora vinklarna är. Då blir svaret (c), det går inte att avgöra. För den som känner sig osäker, går det bra att räkna lite snabbt. Då kan det vara bra att markera lite fler vinklar.

I fall ett får vi att: 

Eftersom sträckan EH utgör en höjd/normal till triangelns sida BC, kan vi säkert säga att vinkeln BEH är rät. Det innebär att vinkeln HBE måste vara 45°, eftersom vinkeln BHE är 45°. Samma logik kan appliceras på den triangel som bildats av punkterna C, E och H. Sträckan BF utgör en höjd till triangelns sida AC, vilket innebär att vinkeln BFC också är rät. Eftersom vinkeln CBF (samma som BHE) är 45°, måste även vinkeln BCF vara 45°. Denna vinkel ligger inom triangeln, och för detta fall stämmer alltså svarsalternativ (a). I en triangel med en 45°-vinkel kan ingen 135°-vinkel finnas, då vinkelsumman då blir för stor för triangeln. Därför kan alternativ (b) inte stämma för denna triangel.

Nu till fall två, där det är de två höjder som inte ligger intill varandra som skär varandra i en 45°-vinkel: 

Fyrhörningen AFHG har vinkelsumman 360°, varav vinklarna AFH och AGH är räta. Dessutom vet vi att vinkeln FHG är 45°, eftersom det är utgångspunkten för detta fall. Detta innebär att vinkeln GAF är 135°, och eftersom BAC och GAF är alternatvinklar, är de lika stora. En vinkel i vår triangel (ABC) är alltså 135°, vilket stämmer med svarsalternativ (b). I en triangel med en 135°-vinkel kan ingen 45°-vinkel finnas, då vinkelsumman då blir för stor för triangeln. Därför kan alternativ (a) inte stämma för denna triangel.

Slutsatsen vi kan dra av detta är att vi har två möjliga situationer när det gäller vilka höjder som utgör den 45°-iga vinkel som krävs i uppgiften, och dessa situationer medför att olika svarsalternativ är korrekta. Vi kan därmed inte säkert säga något om vinklarna i triangeln. 

Svar: (c), det går ej att avgöra.

Uppgifter som liknar denna: 

1. Höjderna i triangeln ABC skär inte varandra, men deras förlängningar skär varandra på så sätt att den största spetsiga vinkel som bildas vid skärningspunkten är 60°. Då kan slutsatsen dras att det i triangeln

(a): finns en trubbig vinkel

(b): finns två lika stora vinklar

(c): det går inte att avgöra vilka typer av vinklar som finns i triangeln

(d): någon sådan triangel finns inte. 

2. I en triangel ABC skär höjderna, eller deras förlängningar, varandra. Då kan slutsatsen dras att

(a): Triangeln innehåller minst två spetsiga vinklar

(b): Triangeln innehåller tre spetsiga vinklar

(c): Triangeln innehåller minst en trubbig vinkel

(d): det går inte att avgöra

20. De fyra punkterna A, B, C och D är olika och ligger i rummet så att trianglarna ABC, BCD, CAD och ABD alla är liksidiga (det vill säga ABCD är en regelbunden tetraeder). Vinkeln mellan de två planen som trianglarna ABC och ABD ligger i är

(a): mindre än 60°

(b): lika med 60°

(c): större än 60°

(d): det går inte att avgöra

Denna uppgift kan lösas på flera olika sätt, både geometriskt och algebraiskt. För enkelhetens skull kan vi sätta sidlängden till 1. 

Den vinkel vi vill hitta är vinkeln mellan två sidor. Genom att bilda en triangel som går från ett hörn, till mittpunkten på motstående sida, upp till det övre hörnet, och tillbaka längs sidan ned till utgångspunkten, får vi en triangel som innehåller just denna vinkel, nedan markerad med x.  

Denna triangel har en sida med sidlängs 1, och två sidor som utgörs av höjden i varsin (identisk) triangel. 

Höjden i en triangel är aldrig lika lång som dess sida. Det innebär att vår triangel ADE inte är liksidig, och att vinkeln x därför inte kan vara 60°, vilket utesluter alternativ (b). 

För den som känner sig bekväm med geometrin, kan vi redan här hitta svaret, utan fler beräkningar. Sidorna som utgörs av höjder (DE och AE) är kortare än sträckan AD. Om vi skulle utgå från en liksidig triangel, med vinkeln 60°, och sedan förkorta två av sidorna lika mycket, vad händer då med vinkeln mellan dessa två sidor? 

För den som gärna vill räkna, kan cosinussatsen användas. Sidorna AE och DE utgör som sagt höjder i sina trianglar, och eftersom det är en regelbunden tetraeder, är dessa liksidiga. Deras sidlängder är ett, som vi bestämde. Detta medför att vi kan beräkna längden av sidorna AE och DE till $\frac{\sqrt{3}}{2}$, med hjälp av Pythagoras sats. 

Cosinussatsen säger att en triangel med sidorna a, b och c uppfyller sambandet $a^2=b^2+c^2-2bc·\cos \left(\alpha \right)$, där vinkeln alfa är vinkeln mittemot sidan a. I vårt fall innebär detta att $a=1$, $b=c=\frac{\sqrt{3}}{2}$, och $\alpha=x$. Cosinussatsen ger då: 

$$\begin{gathered} 1^2={\left(\frac{\sqrt{3}}{2}\right)}^2+{\left(\frac{\sqrt{3}}{2}\right)}^2-2\left(\frac{\sqrt{3}}{2}\right)\left(\frac{\sqrt{3}}{2}\right)·\cos \left(x\right) \\ 1=2{\left(\frac{\sqrt{3}}{2}\right)}^2\left(1-\cos \left(x\right)\right) \\ -\frac{2}{3}+1=\cos \left(x\right) \\ x=\arccos \left(\frac{1}{3}\right) \end{gathered}$$

Exakt vad arccosinus av 1/3 är, behöver vi inte veta eller beräkna. Det räcker med att notera att $\cos (60°)=\frac{1}{2}$ och $\cos (90°)=0$, samt att cosinusfunktionen inte vänder mellan 60° och 90°. En tredjedel är mindre än en halv, vilket innebär att cos(x) i vårt fall ligger närmare 90° än vad vinkeln 60° gör. Svaret blir då (c), större än 60°. 

Det går även att utgå från höjden i tetraedern: 

Här är det vinkeln FHI som vi är intresserade av. Om vi hittar längden av HI och FH, kan vi beräkna storleken av denna vinkel. För tydlighetens skull, kan det vara bra att sätta ut några extra linjer och vinklar: 

Vinkeln y är halva vinkeln i en liksidig triangel, och är därför 30°. Sträckan HB är hälften av tetraederns sidlängder, vilket blir 1/2, då vi satte sidlängden till 1. Då gäller sambandet: 

$$\begin{gathered} \tan (30°)=\frac{\left|HI\right|}{\left|HB\right|}=\frac{\left|HI\right|}{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}} \\ \left|HI\right|=\frac{1}{2}·\frac{\sin (30°)}{\cos (30°)}=\frac{1}{2}·\frac{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{{\displaystyle \raisebox{1ex}{$\sqrt{3}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}=\frac{1}{2\sqrt{3}} \end{gathered}$$

Sträckan FH kan beräknas med Pythagoras sats, och fås då till $\frac{\sqrt{3}}{2}$. Då gäller sambandet: 

$\cos \left(x\right)=\frac{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2\sqrt{3}$}\right.}}{{\displaystyle \raisebox{1ex}{$\sqrt{3}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}=\frac{1}{3}$

Precis som när vi använde cosinussatsen ovan, räcker det med att notera att $\cos (60°)=\frac{1}{2}$ och $\cos (90°)=0$, samt att cosinusfunktionen inte vänder mellan 60° och 90°. Vi kan därmed dra slutsatsen att x måste vara större än 60°.

Svar: (c), större än 60°. 

Uppgifter som liknar denna: 

1. En kon med höjden 3 längdenheter har enhetscirkeln som bas. Inuti konen placeras en maximalt stor cylinder stående (med cirkelytorna parallella med enhetscirkeln), så att en mindre kon bildas inuti konen. Vinkeln mellan det plan som den mindre konens botten ligger i, och de linjer som utgör konens väggar är

(a): mindre än 60°

(b): lika med 60°

(c): större än 60°

(d): det går inte att avgöra

2. Kvadraten ABCD har sidan 3. En punkt E, som ligger inuti kvadraten ABCD dras rakt uppåt (vinkelrätt mot kvadraten) för att bilda en pyramid ABCDE. Vinkeln ACE är

(a): mindre än 90°

(b): lika med 90°

(c): större än 90°

(d): det går inte att avgöra

21. Beräkna

$\frac{{\displaystyle \frac{16}{5}}-{\displaystyle \frac{4}{3}}}{{\displaystyle \frac{2}{15}}+{\displaystyle \frac{3}{2}}}$

Ange svaret på formen $\frac{p}{q}$, där p, q är heltal och bråket $\frac{p}{q}$ är maximalt förkortat. 

Här är det vanlig bråkräkning som behövs. Minsta gemensamma nämnare för bråken i täljaren är 15, och för bråken i nämnaren är minsta gemensamma nämnare 30. Det går ofta bra att, om nämnarna inte är allt för stora, förlänga till produkten av nämnarna, även om det finns en mindre gemensam nämnare. För bråk med täljare 8 och 6 går det bra att förlänga till $8\cdot6=48$, även om minsta gemensamma nämnare är 24. 

$\frac{{\displaystyle \frac{16·3}{5·3}}-{\displaystyle \frac{4·5}{3·5}}}{{\displaystyle \frac{2·2}{15·2}}+{\displaystyle \frac{3·15}{2·15}}}=\frac{{\displaystyle \frac{48}{15}-\frac{20}{15}}}{{\displaystyle \frac{4}{30}+\frac{45}{30}}}=\frac{{\displaystyle \frac{28}{15}}}{{\displaystyle \frac{49}{30}}}=\frac{28·30}{15·49}$

Primtalsfaktorisering är användbart för att förenkla bråket: 

$\frac{28·30}{15·49}=\frac{\left(2·2·7\right)·\left(2·3·5\right)}{\left(3·5\right)·\left(7·7\right)}=\frac{\left(2·2·\bcancel{7}\right)·\left(2·\bcancel{3·5}\right)}{\bcancel{\left(3·5\right)}·\left(\bcancel{7}·7\right)}=\frac{8}{7}$

Svar: $\frac{8}{7}$.

Uppgifter som liknar denna: 

1. Beräkna

$\frac{{\displaystyle \frac{12}{7}}-{\displaystyle \frac{27}{6}}}{{\displaystyle \frac{13}{26}}-{\displaystyle \frac{2}{14}}}$