Matematik- och fysikprovet 2016 fråga 17
https://gyazo.com/6c320ab1822c4d5c235b34e6a9e3e660

Behöver verkligen hjälp med den här frågan. Jag har tidigare frågat min fysik lärare om den här frågan men han kunde det inte heller.
Svaret enligt facit är https://gyazo.com/e9480d5f4b83659dbcf0fe451a5e4929
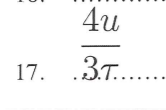
Tack i förväg
La in bilderna åt dig, för att öka chansen att någon skall hjälpa till. /Smaragdalena, moderator
Vektoralgebra från Ma1c kombinerat med begrepp från rörelseläran (kinematiken) i fysik 1, specifikt medelhastighet och centralrörelse.
- Medelaccelleration under ett tidsintervall av längd är definierat som skillnaden i hastighet mellan start och slutpunkt dividerat med tidsintervallets längd
- Vid cirkelrörelse är beloppet av hastighetsvektorn konstant , för hastigheter vid alla tidpunkter under rörelsen. Endast riktning varierar.
- Vid tiden har partikeln rört sig 3/4 av ett varv dvs 270o eller motsvarande antal radianer.
Dessa idéer i kombination med att rita upp en bild som illustrerar de två tillstånden vid t = 0 och t = (3/2)tau är tillräckligt för att lösa problemet.
Siffrorna i punkt två om vinklar har blivit knasiga. Bortse från den.
Personligen tror jag att din lärare visst kan lösa uppgiften.
Ja, han kan nog göra det, men det finns ju i alla fall två troliga alternativ (1) läraren är bra på att motivera genom att ibland låtsas som att han inte kan så att eleven kan känna sig stolt över att angripa saker själv [jag önskar att jag kunde göra det] eller (2) läraren förstod inte frågan. Att man ska åberopa en teknisk definition av medelacceleration långt utanför dess giltighetsdomän är en knasighet i mina ögon även om jag gör det utan att blinka.
(Förutsatt att hej verkligen har frågat sin lärare)
SeriousCephalopod skrev:Vektoralgebra från Ma1c kombinerat med begrepp från rörelseläran (kinematiken) i fysik 1, specifikt medelhastighet och centralrörelse.
- Medelaccelleration under ett tidsintervall av längd är definierat som skillnaden i hastighet mellan start och slutpunkt dividerat med tidsintervallets längd
- Vid cirkelrörelse är beloppet av hastighetsvektorn konstant , för hastigheter vid alla tidpunkter under rörelsen. Endast riktning varierar.
- Vid tiden har partikeln rört sig 3/4 av ett varv dvs 270o eller motsvarande antal radianer.
Dessa idéer i kombination med att rita upp en bild som illustrerar de två tillstånden vid t = 0 och t = (3/2)tau är tillräckligt för att lösa problemet.
Hej sitter fast på samma uppgift. Hur kommer det sig att partikeln har rört sig vid tidpunkten förstår inte riktigt hur, tack.
@indhelpmathematica Jag kan inte redigera det längre. Mitt andra inlägg från i morse klargör att jag har skrivit fel på mer eller mindre alla siffror i just den punkten så borde stå något i stil med
Vid tiden (3/2)τ har partikeln rört sig 3/2 av ett varv dvs 540 grader eller motsvarande antal radianer. (Ett och ett halvt varv)
istället.
SeriousCephalopod skrev:@indhelpmathematica Jag kan inte redigera det längre. Mitt andra inlägg från i morse klargör att jag har skrivit fel på mer eller mindre alla siffror i just den punkten så borde stå något i stil med
Vid tiden (3/2)τ har partikeln rört sig 3/2 av ett varv dvs 540 grader eller motsvarande antal radianer. (Ett och ett halvt varv)
istället.
Tack nu förstår jag hur man ska tänka. Ber om ursäkt att jag inte såg ditt inlägg som kom efter.
SeriousCephalopod skrev:Vektoralgebra från Ma1c kombinerat med begrepp från rörelseläran (kinematiken) i fysik 1, specifikt medelhastighet och centralrörelse.
- Medelaccelleration under ett tidsintervall av längd är definierat som skillnaden i hastighet mellan start och slutpunkt dividerat med tidsintervallets längd
- Vid cirkelrörelse är beloppet av hastighetsvektorn konstant , för hastigheter vid alla tidpunkter under rörelsen. Endast riktning varierar.
- Vid tiden har partikeln rört sig 3/4 av ett varv dvs 270o eller motsvarande antal radianer.
Dessa idéer i kombination med att rita upp en bild som illustrerar de två tillstånden vid t = 0 och t = (3/2)tau är tillräckligt för att lösa problemet.
Tack så mycket förstår nu
Kan man inte tänka att V0=u och Vf=-u och tiden det tog var 3T/2
V0=Vf+at
ger a=-4u/3T
Absolut. Så kan man göra.



