Matematik, geometri cirkel problem

Jag har försökt testat mig runt hur jag ska lösa de här men mitt svar blir alltid fel. Jag vet inte riktigt hur man ska rita upp den här!
Börja med att rita upp en irkel oh markera tre punkter på den, ar som helst. Kalla dem A, B och C. Markera också mittpunkten M. Det står att medelpunktsvinkeln som hör ihop med cirkelbågen AB är 150o. Skriv in det! Det står också (fast otydligt) att medelpunktsvinkeln till cirkelbågen BC är 90o. Nu vet du tillräckligt för att beräkna storleken på bågvinklarna och C. Vinkeln B får du genom vinkelsumman i en triangel. Vad kommer du fram till för vinklar?
Om du vill kan du rita en ny figur med mer korrekta vinklar. Det är helt OK att det blir fel i den första skissen.

Jag testade mig fram till de här. Jag kom alltså fram till dessa tre vinklar, 90, 120, 150 vilket blir 360 totalt i cirklen.
Det finns ingen anledning att testa. Du har skrivit in ett antal vinklar som man inte frågar efter - varför?
Vad jag kan se har du inte ritat upp trianglen AB - det finns ingen linje mellan A och B.
Gör en ny cirkel dät man kan se att vinkeln AMB är 150 gradet och att BMC är 90 grader. Eftersom du vet medelpunktsvinklarna till alla tre cirkelbågarna borde det vara lätt att beräkna randvinklarna A, B respektive C. Hur stora är de tre vinklarna?
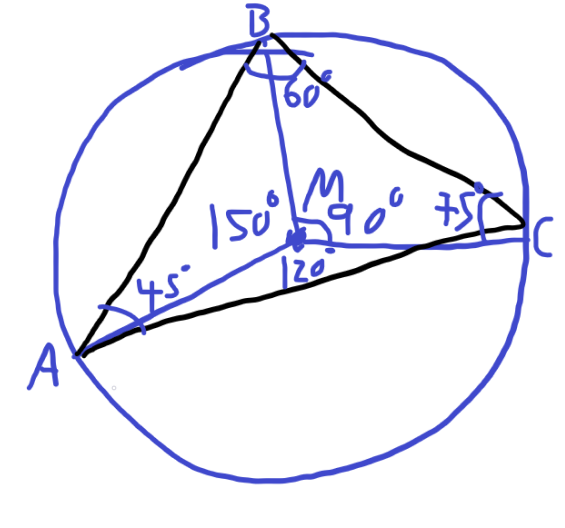
Menar du så här? Jag beräknade randvinklarna och kom fram till detta. Så i den här triangeln är A = 45, B = 60, C = 75
Här ser alla tre medelpunktsvinklarna ut att vara 120 grader. Gör en bättre bild!
Vinklarna blir 90°, 120° och 150°.
Areasatsen ger att arean är
1/2 r^2 sin(90°) + 1/2 r^2 sin(120°) + 1/2 r^2 sin(150°)
= 1/2 r^2 ( sin(90°) + sin(120°) + sin(150°) )
= 1/2 r^2 ( sin(90°) + sin(60°) + sin(30°) )
= 1/2 2^2 ( 1 + sqrt(3)/2 + 1/2 )
= 3 + sqrt(3) a.e.
Trinity2 skrev:Vinklarna blir 90°, 120° och 150°.
Areasatsen ger att arean är
1/2 r^2 sin(90°) + 1/2 r^2 sin(120°) + 1/2 r^2 sin(150°)
= 1/2 r^2 ( sin(90°) + sin(120°) + sin(150°) )
= 1/2 r^2 ( sin(90°) + sin(60°) + sin(30°) )
= 1/2 2^2 ( 1 + sqrt(3)/2 + 1/2 )
= 3 + sqrt(3) a.e.
Areasatsen lär man sig i Ma3, men den här tråden ligger i Ma2, så det borde finnas något annat sätt.
Ja men okej, nu ser jag att vinklarna i randvinkeln blir 90, 120, 150 på bilden jag ritade upp. Men hur ska jag kunna veta längden på dessa sträck när jag vet att radien är 2.0cm? Tacksam för svar!
Smaragdalena skrev:Trinity2 skrev:Vinklarna blir 90°, 120° och 150°.
Areasatsen ger att arean är
1/2 r^2 sin(90°) + 1/2 r^2 sin(120°) + 1/2 r^2 sin(150°)
= 1/2 r^2 ( sin(90°) + sin(120°) + sin(150°) )
= 1/2 r^2 ( sin(90°) + sin(60°) + sin(30°) )
= 1/2 2^2 ( 1 + sqrt(3)/2 + 1/2 )
= 3 + sqrt(3) a.e.
Areasatsen lär man sig i Ma3, men den här tråden ligger i Ma2, så det borde finnas något annat sätt.
Tack för det. Såg inte att det var Ma2. Det går att lösa genom att förlänga en av radierna som bildar 150° och därmed blir komplementet 30° och resten är lätt.
Men jag förstår inte riktigt hur de skulle hjälpa mig. Om jag skulle förlänga A i detta fal hur blir komplementet 30° och hur ska jag kunna få detta i CM på längden?
Hjälper denna ritning dig?

Arean av 90°-triangeln klarar du lätt.
Arean av 120°-triangeln klarar du också lätt. Det är 2 st. halva liksidiga trianglar.
Arean av 150°-triangeln gör du på följande sätt:
Drag ut radien som visat ovan streckad linje.
Den lodräta radien bildar då 180°-150°=30° med den streckade linjen.
Drag sedan den streckade höjden. Hur lång är denna höjd om den lodräta radien är 2?
Du kan nu räkna ut 150°-triangelns area.
Summera sedan de tre trianglarnas areor och du har ditt svar.
Men Arean på 90° hittas väldigt enkelt men hur kan det vara lätt att hitta arean på 120° triangeln. Det går inte ihop eftersom vi inte vet hur lång den nedre sträckan är. Det går ju inte att använda pythagoras satsen eller något liknande eftersom det måste vara 90°.
Dela 120°-triangeln i två delar.
Arean av en halv liksidig triangel är enkel.
Men grejen är om vi har en halvliksidig triangel vet vi ju inte längden på alla sidor utan bara 1 av dem. Kolla på följande bild:
Det som vi vill beräkna är ju längden på Y. Men den enda längsidan vi har ett konkret svar på är sidan där jag skrev 2. Vi vet inte mitten linjen om den är 1, 1.2 eller 1.3 eller 1.4 osv.
Hur stora är vinklarna och sidorna i den röda triangeln?


Vi kan väl inte få längden på de andra två sidorna i den röda triangeln?
Jo, det är en 30-60-90-triangeln och du känner då till förhållandet mellan sidorna.
30-60-90-triangeln är en halv liksidig triangeln och vad gäller för en liksidig triangel?
Titta i din lärobok.

Okej okej så här långt har jag förstått. Jag vet att cirkeln är färgbombad men Arean för den röda trianglen är 0.87 och det gånger två så får vi 120 grader trianglen. Så nu har vi arean för 2 av de 3 trianglarna. vi har A1 = 2 cm^2 och A2 = 1.74 cm^2 men jag har väldigt svårt att komma fram härifrån. Som du ser har jag räknat lite till vinklar om det kanske hjälper. För den osynliga linjen ritat hjälper oss väl inte att räkna arean eftersom den går utan självaste hela trianglen. För enligt boken så är svaret 26cm^2
Svaret kan omöjligen vara 26 cm^2. Det är 13 gånger så stort som den rätvinkliga triangeln.
Men du har nu gjort 2/3 av uppgiften.
2 cm^2 är rätt på den rätvinkliga triangeln
Den röda triangeln har arean sqrt(3)/2 (vad du beräknar till 0.87) och då har hela den nedre triangeln arean sqrt(3)≈1.73 cm^2.
Så långt allt rätt.
Kvar återstår den vänstra triangeln. Den sida som pekar rakt upp, mot B vet du är 2.
Du har också märkt ut korrekta vinklar i den triangeln, 30-60-90. Vad kan du nu säga om den sidan som står mot 30°? Den påminner om den röda triangeln, eller hur?
Svaret enligt boken måste vara fel. Men jag kan fortsätta försöka sen prata med läraren! Tack så mycket för hjälpen förresten!
Den nya triangeln som formas kan man göra exakt som den förra. Så då får vi en area på 0.87cm^2 i den triangeln som har 30, 60 och 90 grader. Men vad blir då nästa steg när man vet arean på en triangel som stiger utanför triangelns area vi vill räkna ut?
Ni vet du att höjden är 1 i den "utanliggande" triangeln. Den här även höjd till 150°-triangeln som har en radie som bas och då kan du räkna ut dess area 1/2 bh = ...
Nu har du arean för alla tre och du kan summera dem.

YESS, blir detta då korrekt. Jag förstår stegen nu men det var extremt mycket. Tack för all hjälpen. Det uppskattas :)
Mycket bra!
Du får pluspoäng om du svarar exakt som 3+sqrt(3).
(Som anmärkning kan du kommentera att areorna för de tre trianglarna, 1, 2 och sqrt(3) förhåller sig på samma sätt som sidorna i en halv liksidig triangel, som där är 1, 2 och sqrt(3).)
Tack så hemskt mycket, väldigt nöjd med hjälpen! :)



