Matematik 5000+ (för reviderad ämnesplan) matematik 4 Kap 3 Blandade övningar kap 3 uppgift 9
Hej, jag har en uppgift som jag försöker lösa och har fastnat. Det är uppgit 9 som jag ska lösa och jag har fått fram att skärningspunkten är k (i x-led) har sedan försökt räkna ut de båda kurvornas derivator och kommit fram till att den röda blir x^3/3 ochh den blå x^k (vilket känns fel). Sedan har jag satt upp en ekvation med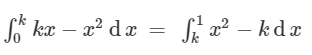 
(kx i den sista ekvationen). Det blir sedan fel från detta stadiet då jag behöver räkna ut dete exakta värdet på k för att sedan kunna sätta in det i en formel för att kuna räkna ut derivaatan. Så min fråga är hur jag ska derivera kx och vad som blir fel i uträkningen oven.
- I den andra integralen har du väl glömt ett x. Integranden bör väl vara x2-kx. Uppgiften är lite förrädisk för vad är det som säger att delningspunkten ligger precis vid kurvornas skärningspunkt? Allt vi vet är att områdenas areor är lika. Att stötta sig på figuren kan straffa sig, men om det gör det i just denna uppgiften vill jag låta vara osagt. Om delningen inte är i skärningspunkten så blir uppgiften mycket mödosam.
Tomten skrev: Integranden bör väl vara x2-kx.
Det var det jag menade med parantensen efter bilden.
Och jag antar att skärnningspunkten ligger på delningspunkten, då uppgiften annars hade varit irrelevant med den preseterade bilden.
Vi antar att fig stämmer. Uppgiften är att bestämma de två lika areorna som vi kallar A1 och A2 (=A) fr vänster räknat. Har ej integraltecken så jag använder |ab som beteckning.
A1=|0k(kx-x2)=…..
A2=|k1(x2-kx)=……
Räkna ut integralerna, sätt dem lika för att bestämma k och sätt in det funna k-värdet i någondera integral för att bestämma dess värde. Du behöver inte derivera någonstans. Bara bestämma primitiva fkner.
Bror, derivatan av den primitiva funktionen är funktionens grundform 💀🤡
