Matematik 3c area
Frågan lyder:
En rektangel har två hörn på kurvan y=9-3x^2 och två hörn på x-axeln. Bestäm det största värde som rektangelns area kan anta. Avgör också om den maximala arean upptar mer än hälften av arean av området mellan kurvan och X-axeln.
Vet inte riktigt hur jag ska tänka.
Börja med att rita!
Anta att rektangelns ena hörn ligger på (a, 0), var ligger då de andra?
Skapa ett uttryck för arean och sök max!
Ture skrev:Börja med att rita!
Anta att rektangelns ena hörn ligger på (a, 0), var ligger då de andra?
Skapa ett uttryck för arean och sök max!
 Är verkligen inte säker men såhär har jag kommit fram till så länge. Undrar även om höjden blir 9-3x^2 då rektangeln har två hörn där och om basen är 6x?
Är verkligen inte säker men såhär har jag kommit fram till så länge. Undrar även om höjden blir 9-3x^2 då rektangeln har två hörn där och om basen är 6x?
om nedra högra hörnet har x-värdet = a (y = 0)
så är övre högra hörnet i koordinaten (a, (9-a2))
Hur stor är då rektangelarean, uttryckt i a?
Ture skrev:om nedra högra hörnet har x-värdet = a (y = 0)
så är övre högra hörnet i koordinaten (a, (9-a2))
Hur stor är då rektangelarean, uttryckt i a?
2a*(9-3a2) ?
ja,
A(a) = 2a*(9-3a2)
och hur hittar du största värde för den funktionen ?
Ture skrev:ja,
A(a) = 2a*(9-3a2)
och hur hittar du största värde för den funktionen ?
Antar att man deriverar funktionen och hittar derivatans nollställen och sedan hitta y-värdet för nollställena och se vilket y-värde som är störst
Låter som en bra plan! Vad får du då?
Ture skrev:Låter som en bra plan! Vad får du då?
Jag får 12 a.e. Men jag fattar dock inte hur jag avgör om den maximala arean upptar mer än hälften av arean av området mellan kurvan och X-axeln.
Har du lärt dig integrera eller kommer det i senare kurs?
Om inte, uppskatta arean under andragradskurvan, exvis genom att lägga en rektangel utanför
Ture skrev:Har du lärt dig integrera eller kommer det i senare kurs?
Om inte, uppskatta arean under andragradskurvan, exvis genom att lägga en rektangel utanför
Ja vi har lärt oss att integrera. Ska jag ställa upp en integral för funktionen?
Ja, och beräkna den!
Ture skrev:Ja, och beräkna den!
är det för kurvan y=9-3a2 då?
Nja, (9-3x2 ) dx
Vilja gränser tänker du integrera mellan?
Ture skrev:Nja, (9-3x2 ) dx
Vilja gränser tänker du integrera mellan?
Kurvans nollställen. X=±√3.
Bra, fortsätt!
Har även en till fråga. Jag fick ju att derivatans nollställen blev x= 1 och x=-1. Jag valde att utesluta x=-1 då punkterna för rektangelns area ligger i första kvadranten. Är det rätt eller borde x=-1 vara med?
Ture skrev:Bra, fortsätt!
Får det till 12√3 a.e. Men vad säger det?
ja vad tycker du, är rektangelns yta större eller mindre än hälften av det du just beräknade?
>På din förra fråga, rektangeln ligger i både första och andra kvadranten.
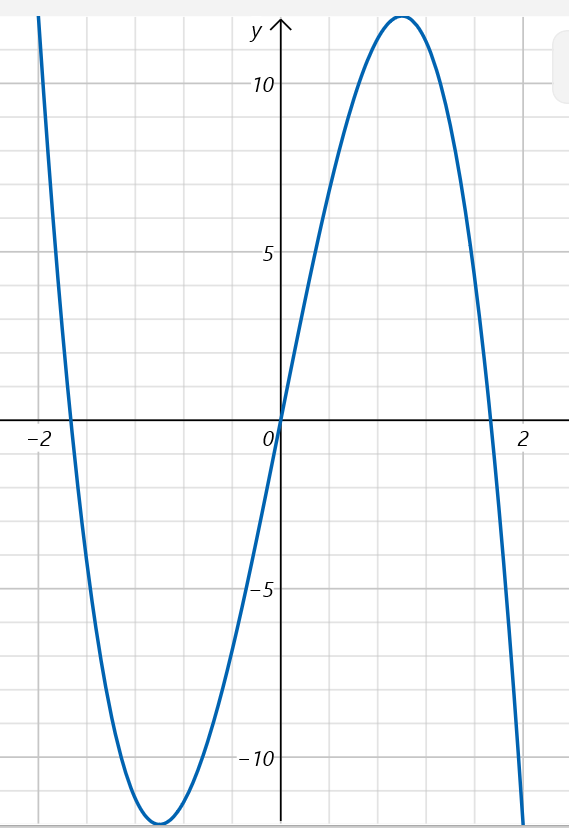
Funktionen som du beräknade extrempunkterna för ser ut så här (2a(9-3a2))
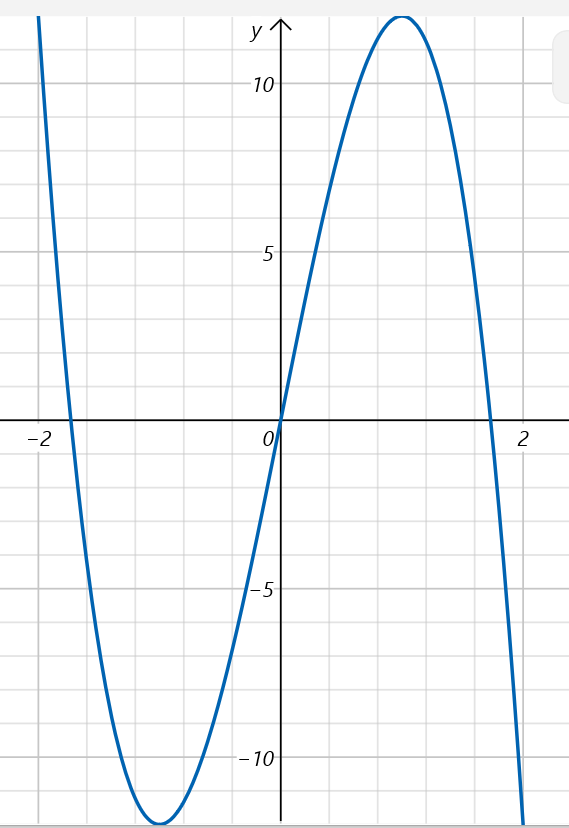
Den har max för +1 och ett min (ointressant för oss) för -1
Ture skrev:ja vad tycker du, är rektangelns yta större eller mindre än hälften av det du just beräknade?
>På din förra fråga, rektangeln ligger i både första och andra kvadranten.
Funktionen som du beräknade extrempunkterna för ser ut så här (2a(9-3a2))
Den har max för +1 och ett min (ointressant för oss) för -1
Den är större än hälften.
Så ska jag även ha med x=-1? Eller fattar inte riktigt. Jag hittade en liknande uppgift som uteslöt x=-1 och blev lite förvirrad nu
När du har deriverat och fått fram derivatans nollställen måste du precis som vanligt avgöra om nollställena är max eller minpunkter.
+1 är ett max för sen funktion jag plottade och - 1 är en minpunkt.
så du ska bara ha med a = 1.
Ej att förväxla med att din rektangel går från x = - 1 till 1
Ture skrev:När du har deriverat och fått fram derivatans nollställen måste du precis som vanligt avgöra om nollställena är max eller minpunkter.
+1 är ett max för sen funktion jag plottade och - 1 är en minpunkt.
så du ska bara ha med a = 1.
Ej att förväxla med att din rektangel går från x = - 1 till 1
Okej jag tror jag förstår nu. Kan jag då med hjälp av en teckentabell visa att x=-1 inte är relevant för oss då det är en minpunkt?
Ture skrev:Ja!
Då förstår jag. Tusen tack för hjälpen!! :)