Massa som skjuts mha. en fjäder nerför en ramp:Hur stor är kraften från fjädern

Hej! Sitter och pluggar inför kommande omtenta i Fysik 1, men har otroligt svårt att komma till en lösning. Bilden nedan visar uppgiften

Min tanke är att antingen använda Mek. energisatsen eller NII-lag. Mek. energ. får jag inte till, kommer inte på något sätt att använda Ug eller K2, kom endast fram till detta: $U e 1 + W ö w r = K 2$

Så har nu försökt med NII. Frilägger lådan och komposantuppdelar krafterna. Friläggningen:

I X-led får jag då:

$k x = m g (\sin (10) + (\cos (10) * μ_{k}))$

och i Y-led: $N = m g \cos (10)$

Men kommer inte fram till något utav svarsalternativen. Minns inte heller om jag behöver göra:

$F = \sqrt{\sum_{}^{} F x^{2} + \sum_{}^{} F y^{2}}$

Har alltid haft svårt för fysik men mattekurserna har jag nu klarat utan några större problem. Skulle vara otroligt skönt att sätta omtentan som går om ungefär en månad, men just nu känns det ganska hopplöst (särskilt när jag inte ens har rätt svar till dessa flervalsfrågor jag sitter och nöter på). All hjälp uppskattas otroligt! :)

EDIT: Det är väl inte så enkelt att kan använda Hooke's lag direkt? 500*0.1= 50N

Jo så enkelt är det. Använd Hooks lag.

PATENTERAMERA skrev:
Jo så enkelt är det. Använd Hooks lag.

Där ser man, kändes för enkelt för att vara sant men ibland är det så.

Dessvärre har jag kört fast på andra delfrågan till denna uppgift: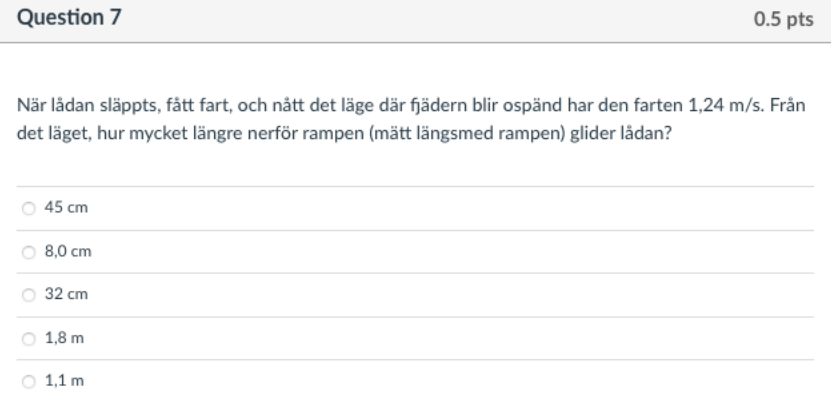

Testade återigen att ställa upp mek. energ. med UG i höger och vänsterled: $U g_{1} + U e_{1} - μ_{k} = U g_{2} + K_{2}$

Landar slutligen i ett utryck för delta h: $∆ h = (\frac{m v^{2}}{2} + μ_{k} * N - \frac{k x^{2}}{2}) / m g$

Och kan då få fram sträckan s: $s = ∆ h * \sin (10)$

Men kommer självklart inte nära nåt utav svarsalternativen och jag antar att det finns något enklare sätt att räkna ut detta.

Det är rätt att tänka att

U_gravitation1 + U_elastisk1 + K₁ = U_gravitation2 + K₂ - Friktionsarbete.

Men U_elastisk1 = 0, eftersom i läge 1 så är fjädern ospänd.

Vidare är K₂ = 0, eftersom lådan är i vila i läge 2.

Friktionsarbete = -s $\cdot$ F_friktion = -s $\cdot$ $μ_{k}$ $\cdot$ N = -s $\cdot$ $μ_{k}$ $\cdot m g \cdot \cos θ$ .

PATENTERAMERA skrev:
Det är rätt att tänka att

U_gravitation1 + U_elastisk1 + K₁ = U_gravitation2 + K₂ - Friktionsarbete.

Men U_elastisk1 = 0, eftersom i läge 1 så är fjädern ospänd.

Vidare är K₂ = 0, eftersom lådan är i vila i läge 2.

Friktionsarbete = -s $\cdot$ F_friktion = -s $\cdot$ $μ_{k}$ $\cdot$ N = -s $\cdot$ $μ_{k}$ $\cdot m g \cdot \cos θ$ .

Okej, jag tänkte att fjädern i läge 1 är spänd (komprimerad) och i läge 2 när den skjuter iväg lådan är den ospänd. Skulle alltså behövt ett läge 3 isåfall, vilket blir onödigt när alla variabler finns.

Borde det inte finnas en friktionskraft eller friktionsarbete vid läge 1 också, som bromsar lådan initialt? Eller har du tänkt den som positiv vid läge 1 och bara flyttat den till HL?

I övrigt så hänger jag med ganska bra. Att använda friktionsarbetet tänkte jag inte på (såg nåt liknande på youtube men kopplade inte hur eller varför han gjorde så). Ska testa att räkna om uppgiften nu!

Landade i $\frac{m v^{2}}{2} = s (μ_{k} m g \cos (10) - m g \sin (10))$ $\overset{}{\to} s = \frac{\frac{m v^{2}}{2}}{m g (μ_{k} \cos (10) - \sin (10))}$ =1.1m

Bra mycket klurigare än första uppgiften. Tog ett tag innan jag insåg att $∆ h = \sin (10) * s$

Känns som rätt svar så jag känner mig nöjd. Men jag förstår fortfarande inte om friktionsarbetet hamnar i läge 1 eller 2, och varför sträckan egentligen är negativ. Spelar ju ingen roll i detta fallet om jag använt +s, men ändå.

Tack för all hjälp @patenteramera!

Friktionsarbetet hamnar inte egentligen i något läge utan utförs då lådan rör sig från läge 1 till läge 2.

Egentligen skulle man kunna skriva

Friktionsarbetet som utförs på lådan då den rör sig mellan läge 1 och 2 = skillnad i mekanisk energi mellan läge 2 och läge 1. Dvs

Friktionsarbete = U₂ + K₂ - (U₁ + K₁). Mekanisk energi = summan av potentiell och kinetisk energi.

Det är inte så att sträckan s skall ses som negativ, men friktionsarbetet blir negativt eftersom friktionskraften verkar i motsatt riktning som förflyttningen. Dvs den mekaniska energin skall minska. Så om vi räknar s och F_friktion som positiva storheter så måste vi ha ett minustecken framför för att få rätt tecken på friktionsarbetet i slutändan.

PATENTERAMERA skrev:
Friktionsarbetet hamnar inte egentligen i något läge utan utförs då lådan rör sig från läge 1 till läge 2.

Egentligen skulle man kunna skriva

Friktionsarbetet som utförs på lådan då den rör sig mellan läge 1 och 2 = skillnad i mekanisk energi mellan läge 2 och läge 1. Dvs

Friktionsarbete = U₂ + K₂ - (U₁ + K₁). Mekanisk energi = summan av potentiell och kinetisk energi.

Det är inte så att sträckan s skall ses som negativ, men friktionsarbetet blir negativt eftersom friktionskraften verkar i motsatt riktning som förflyttningen. Dvs den mekaniska energin skall minska. Så om vi räknar s och F_friktion som positiva storheter så måste vi ha ett minustecken framför för att få rätt tecken på friktionsarbetet i slutändan.

Nu tror jag att jag förstår, superbra förklarat! Stänger tråden men hoppas jag får lika bra hjälp i fortsättningen.

Svara

Visa senaste svar