Magnetiska flödet genom lutande slinga
Hej! Jag har en uppgift som jag inte får rätt på och jag förstår inte vart jag gör fel. Uppgiften lyder: Flödestätheten i ett homogent magnetfält är 350mT. Beräkna det magnetiska flödet genom en rektangulär trådslinga med längden 12 cm och bredden 8,0 cm då slingan bildar vinkeln 30 grader med flödeslinjerna.
Den formel jag har fått lära mig när det handlar om vinklade slingor är att = B x A x cos v
När jag använder denna formel skriver jag då:
och får då svaret 2,9 mWb men svaret enligt facit ska bli 1,7 mWb, men jag förstår inte vad det är jag missar eller gör fel.
Prova med sinus istället för cosinus så får du rätt svar:
350*10^(-3)*0.12*0.08*sin(30)=0.00168
Du får fel svar eftersom vinkeln med flödeslinjerna är 30 grader vilket betyder att v=90-30=60. Som du säkert vet är sin(v)=cos(90-v).
Vinkeln (i ditt fall ) avser vinkeln mellan "svansarna" hos areavektorn och flödestäthetsvektorn. Egentligen är definitionen för flöde:
Den feta punkten är inget multiplikationstecken utan kallas för en skalärprodukt:
Bild tagen från Wikipedia.
Kontentan av det hela är helt enkelt att det var fel vinkel du använde. Men jag tycker frågan är lite tvetydigt ställd. En figur från frågeskaparnas sida hade nog förenklat väldigt mycket.
För att förtydliga varför jag anser frågan vara något tvetydig har jag ritat en liten bild nedan:
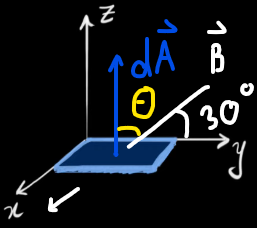
Så här tolkar jag frågan. Men det är ju inte den enda tolkningen av texten.
Okej, jag tror jag förstår. Men är det alltså för att det är den korta kateten i triangeln som bildas som är vinkelrät mot flödeslinjerna och därför är det bara den "delen" av arean som blir träffad av flödestätheten och därmed endast den delen som bidrar till det magnetiska flödet? Och för att få den korta kateten tar man alltså sinus för vinkeln eftersom vi vet hela arean vilket motsvarar hypotenusan i triangeln?
Nej, nu tror jag det har skett något missförstånd. Areavektorn är ingen del av arean utan endast en vektor som är vinkelrät mot ytan och vars längd är proportionell mot areans storlek. Areavektorer är användbara verktyg i fysiken, men de är inga areor i sig. Nu ritade jag bara in en vektor från magnetfältet. Det som är viktigt när det kommer till flöde är den komposant hos magnetfältet som är vinkelrät mot ytan.
Tillägg: 5 maj 2024 12:36
Om jag krånglade till det nu ursäktar jag. Ett lite enklare sätt att beskriva detta på är att:
Tillägg: 5 maj 2024 12:44
Summa summarum är det bara den komposant hos B-fältet som är vinkelrät mot arean som är relevant när man räknar på flöde. Du råkade använde fel vinkel i beräkningen.
Okej, då förstår jag! Tack!



