Magnetisk flödestäthet i DC-krets
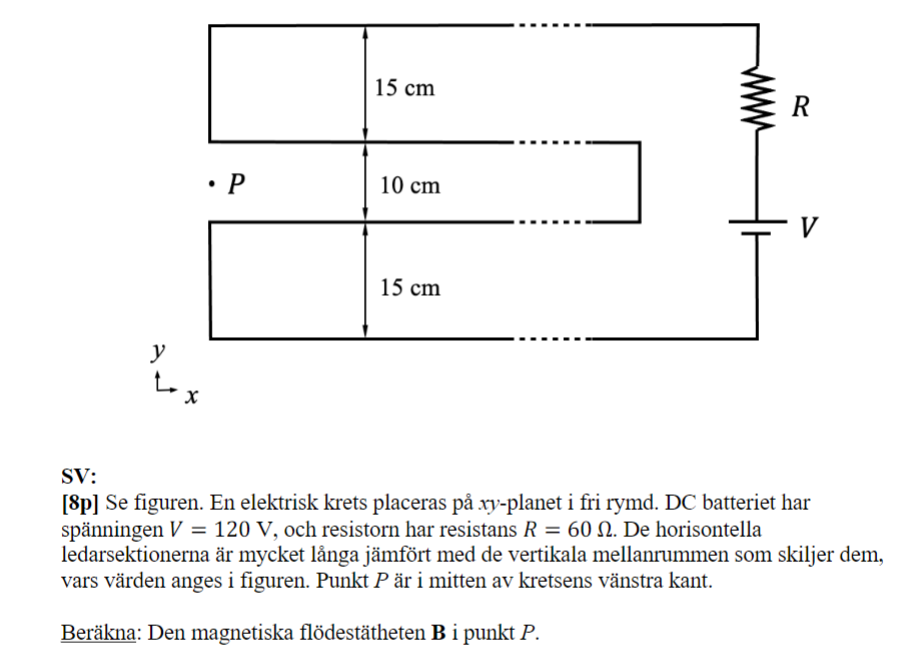
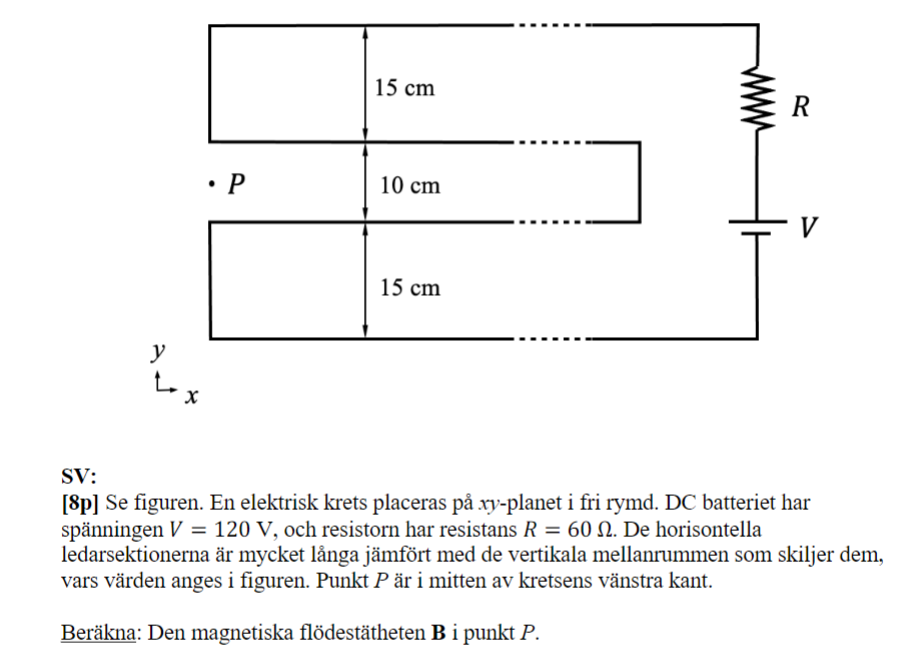
Har problem med att förstå lösningsförslaget till denna uppgift.
När jag räknade kom jag fram till att de två vertikala ledarna inte bidrar till det magnetiska fältet i punkten P, enligt kryssprodukten i Biot-Savarts lag.
Min nästa tanke var att de två sektionerna som består av två ledare var skapar en ledare. Vi behöver endast ta hänsyn till två ledare som, vilket stämmer. Problemet är att jag tänker att dessa två ledare borde gå i mitten av sektionerna med avseende på symmetrin, vilket inte visar sig stämma. Det är i sin tur rimligt, eftersom den magnetiska flödestätheten hade blivit 0 i punkten P. Facit säger att den ena ledaren är placerad 0,2 m från P och den andra 0,05 m. Varför blir det dessa avstånd och inte 0,125 m för båda ledarna?
Keno skrev:
Har problem med att förstå lösningsförslaget till denna uppgift.
När jag räknade kom jag fram till att de två vertikala ledarna inte bidrar till det magnetiska fältet i punkten P, enligt kryssprodukten i Biot-Savarts lag.
Min nästa tanke var att de två sektionerna som består av två ledare var skapar en ledare. Vi behöver endast ta hänsyn till två ledare som, vilket stämmer. Problemet är att jag tänker att dessa två ledare borde gå i mitten av sektionerna med avseende på symmetrin, vilket inte visar sig stämma. Det är i sin tur rimligt, eftersom den magnetiska flödestätheten hade blivit 0 i punkten P. Facit säger att den ena ledaren är placerad 0,2 m från P och den andra 0,05 m. Varför blir det dessa avstånd och inte 0,125 m för båda ledarna?
Det är väl så att magnetfältet från den översta tråden och den nedersta tråden går åt samma håll i punkten P, dessa trådar är bägge på avståndet 0,2
De två inre trådarnas magnetfält verkar oxå åt samma håll, men motsatt de två yttre trådarnas, de inre trådarna har bägge avståndet 0,05.
Det blir tydligare om du ritar bilden från sidan med trådarna som punkter och magnetfälten som cirklar runt resp tråd.