Någon som vet hur man kan börja på uppgift 30?
Det är alltid bra att börja med en skiss:
Vi får en rätvinklig triangel, där den ena sidan är AB1, och den andra sidan är a/2. Hur lång är. AB1? :)
Smutstvätt skrev:Det är alltid bra att börja med en skiss:
Vi får en rätvinklig triangel, där den ena sidan är AB1, och den andra sidan är a/2. Hur lång är. AB1? :)
Ja asså jag ser ej rätvinklig triangel framför mig. Men behöver jag rita en kub alltså och markera att alla sidor är räta samt markera bokstäverna uppgiften ger mig ?
Men behöver jag rita en kub alltså och markera att alla sidor är räta samt markera bokstäverna uppgiften ger mig ?
Ja, det är alltid en bra början! :)
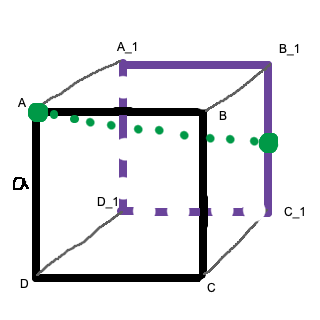
Den rätvinkliga triangeln är lite knepig att se, men dra en linje från A till B1, och sedan från B1 till mitten på sträckan B1C1, och sedan längs den grönprickade linjen i bilden ovan (från mittpunkten vi var på, till A). Det blir en rätvinklig triangel som går snett inåt i pappret. :)
Smutstvätt skrev:Men behöver jag rita en kub alltså och markera att alla sidor är räta samt markera bokstäverna uppgiften ger mig ?
Ja, det är alltid en bra början! :)
Den rätvinkliga triangeln är lite knepig att se, men dra en linje från A till B1, och sedan från B1 till mitten på sträckan B1C1, och sedan längs den grönprickade linjen i bilden ovan (från mittpunkten vi var på, till A). Det blir en rätvinklig triangel som går snett inåt i pappret. :)
Hm nu hänger jag ej med.. Tror vi får ta ett steg i taget. Blev lite för mycket text på en gång. Jag vet ej vad för grön prick du pratar om..
Ingen fara! Din bild ser bra ut. Jag har även ritat en bild i geogebra:

Sträckan vi vill beräkna är den streckade linjen AE.
Vi kan nu se denna sträcka som en hypotenusa. Kateterna är B1E, samt AB1:

Smutstvätt skrev:Ingen fara! Din bild ser bra ut. Jag har även ritat en bild i geogebra:
Sträckan vi vill beräkna är den streckade linjen AE.
Vi kan nu se denna sträcka som en hypotenusa. Kateterna är B1E, samt AB1:
Det kanske är en dum fråga men var kommer E ifrån?
E är mittpunkten på sträckan B1C1. :)
Smutstvätt skrev:E är mittpunkten på sträckan B1C1. :)
ok
Eftersom kubens sidor har längden a, är sträckan B1E lika med a/2 (E ligger på mitten av kubens sida B1C1). Nu behöver vi därför hitta längden av sidan AB1, så att vi kan använda Pythagoras sats för att beräkna längden av sträckan AE. :)
Smutstvätt skrev:Eftersom kubens sidor har längden a, är sträckan B1E lika med a/2 (E ligger på mitten av kubens sida B1C1). Nu behöver vi därför hitta längden av sidan AB1, så att vi kan använda Pythagoras sats för att beräkna längden av sträckan AE. :)
Hm jag hänger ej med
Ser du hur vi har en rätvinklig triangel i figuren? Den räta vinkeln ligger vid B1. 
Smutstvätt skrev:Ser du hur vi har en rätvinklig triangel i figuren? Den räta vinkeln ligger vid B1.
Hm ab1 är en diagnol till kvadraten AA1BB1?
Ja precis! (för att vara petig AA1B1B, men jag förstår vad du menar :D)
Smutstvätt skrev:Ja precis! (för att vara petig AA1B1B, men jag förstår vad du menar :D)
Ok. Sträckan B1E är väl a/2? Då blir Ab1 roten ur 2*a. Men jag ser ej att vi ska använda Pythagoras sats för att bestämma AE
Triangeln AB1E är rätvinklig, som nämnts ovan. Du har AB1 och B1E så AE beräknas med Pythagoras.
rapidos skrev:Triangeln AB1E är rätvinklig, som nämnts ovan. Du har AB1 och B1E så AE beräknas med Pythagoras.
Okej om vi får reda på AE så är det svaret på frågan?
Japp. :)







