MaFy-provet 2024 – uppgift 6

Den här krävde lite tankeverksamhet för mig. Alla andra årgångar har det varit tämligen enkla algebraiska operationer för att finna svaret, men denna grundar sig på den omvända triangelolikheten eller, som Smutstvätt ovan, val av listiga värden. I en annan tråd framfördes synpunkten att uppgifterna med a-d-svar var mera av "intuitiv art". Jag är tveksam för denna uppgift. Den är inte intuitiv för mig. Har provet blivit svårare med åren? Att sitta i lugn och ro och fundera med te och kaka är en sak, tidspress en helt annan.

Jag fiskade lite på nätet och fann denna, som jag inte tycker är speciellt bra

Hur kommer han fram till detta?

Om han har likhet, hur får han olikhet? Euklides bevis är mycket intressantare, om än begränsat till plangeometri.

Är det någon som kan förtydliga detta bevis och klargöra vad han menar? Tack.

PS. i samma skrift förekommer detta (författaren eller student? vem vet?)

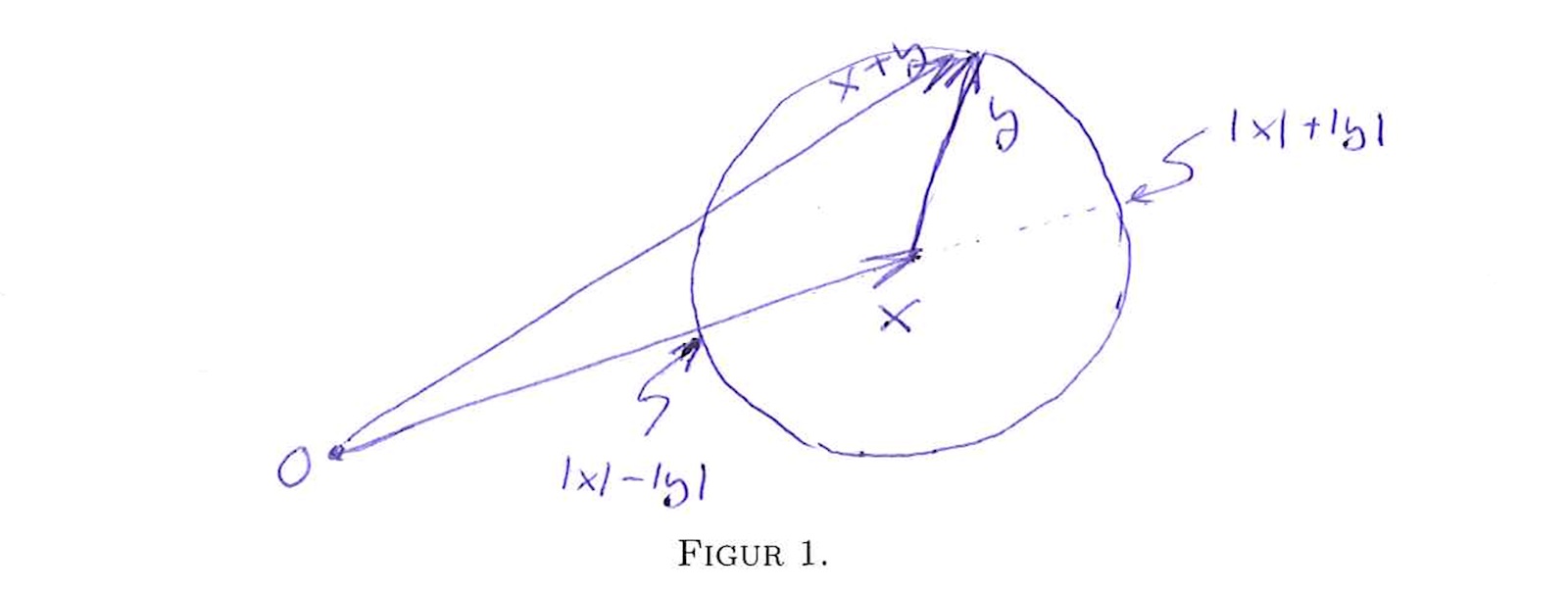
som är en snygg illustration.

Smutstvätt skrev:

Summor av absolutbelopp är alltid större än eller lika med absolutbelopp av en summa, $\left|x+y\right|\le \left|x\right|+\left|y\right|$. 

För att förtydliga denna bit: satsen som används, triangelolikheten ($\left|x+y\right|\le \left|x\right|+\left|y\right|$), kan bevisas på många sätt, men exempelvis genom att undersöka vad som händer när x respektive y är positivt och negativt. 

Värdet av högerledet, $|x|+|y|$ påverkas inte av vilka tecken x respektive y har, utan endast deras belopp. Men vänsterledets värde förändras beroende på tecknen:

• Om x och y båda är positiva, då kommer $x+y$ att ha samma värde som $|x+y|$. $|x|$ kommer att ha samma värde som x, och $|y|$ har samma värde som y. Här gäller därför att $\left|x+y\right|=\left|x\right|+\left|y\right|$. 
• Om x är positivt, men y negativt, då kommer $|x+y|$ att vara mindre än $|x|$. Eftersom att $|y|$ aldrig är negativt, måste då $|x+y|$ vara mindre än $|x|+|y|$. 
• Om x är negativt, men y positivt, då kommer $|x+y|$ att vara mindre än $|y|$. Eftersom att $|x|$ aldrig är negativt, måste då $|x+y|$ vara mindre än $|x|+|y|$. 
• Om x och y båda är negativa, då kommer $x+y$ att ha samma belopp som $|x+y|$, men värdet är negativt. Då spelar det återigen ingen roll om vi applicerar absolutbeloppet först, och summerar sedan, eller om vi summerar först och applicerar absolutbeloppet efteråt. Även här gäller därför att $\left|x+y\right|=\left|x\right|+\left|y\right|$. 
• Om x eller y (eller båda) är noll, försvinner den termen, och kvar blir $\left|x+0\right|=\left|x\right|+\left|0\right|$, eller vice versa för y. 

Vilka värden x och y än har, kan vi därför dra slutsatsen att $|x+y|$ alltid är mindre än eller lika med $|x|+|y|$. 

Det innebär att $-\left|\left|x+y\right|-\left|y\right|\right|$ är mindre än $-\left|\left|x\right|+\left|y\right|-\left|y\right|\right|$ (på grund av minustecknet, på samma sätt som att -5 är mindre än -2). Därmed kan vi konstatera att $\left|x\right|-\left|\left|x+y\right|-\left|y\right|\right|\ge \left|x\right|-\left|\left|x\right|+\left|y\right|-\left|y\right|\right|=\left|x\right|-\left|x\right|=0$. (c) är alltså rätt svar. 

Här appliceras triangelolikheten på uttrycket inuti det innersta absolutbeloppet, $\left|x+y\right|$. Triangelolikheten säger att detta värde är mindre än $\left|x\right|+\left|y\right|$, men! Hela uttrycket ($\left|\left|x+y\right|-\left|y\right|\right|$) föregås av ett minustecken, vilket gör att, om detta uttryckets värde ökar, kommer hela ledets totala värde att minska. Hela ledet är: 

$\left|x\right|-\left|\left|x+y\right|-\left|y\right|\right|$

Så om $\left|\left|x+y\right|-\left|y\right|\right|$ ökar i värde, blir $\left|x\right|-\left|\left|x+y\right|-\left|y\right|\right|$ mindre. Vi kan därför säga att: 

$x⊞y=\left|x\right|-\left|\left|x+y\right|-\left|y\right|\right| \mathbf{\ge }\mathbf{ }\mathbf{ }\mathbf{\left|}\mathit{x}\mathbf{\right|}\mathbf{-}\mathbf{|}\mathbf{\left|}\mathbf{x}\mathbf{\right|}\mathbf{+}\mathbf{\left|}\mathbf{y}\mathbf{\right|}\mathbf{-}\mathbf{\left|}\mathbf{y}\mathbf{\right|}\mathbf{|}$

Härifrån kan vi förenkla: 

$$\begin{gathered} x⊞y=\left|x\right|-\left|\left|x+y\right|-\left|y\right|\right| \mathbf{\ge }\mathbf{ }\mathbf{ }\mathbf{\left|}\mathit{x}\mathbf{\right|}\mathbf{-}\mathbf{|}\mathbf{\left|}\mathbf{x}\mathbf{\right|}\mathbf{+}\mathbf{\left|}\mathbf{y}\mathbf{\right|}\mathbf{-}\mathbf{\left|}\mathbf{y}\mathbf{\right|}\mathbf{|}\mathbf{=} \\ \left|x\right|-\left|\left|x\right|\right|=0 \end{gathered}$$

Och då har vi nått fram till att $x⊞y\ge 0$. :)