mafy 2024 fråga 19
Hej, jag behöver hjälp med fråga 19! Jag förstår varför Pa= p då i ett system ska vätska i samma höjd alltid ha samma tryck. Fattar dock inte hur man kommer fram till Pb. 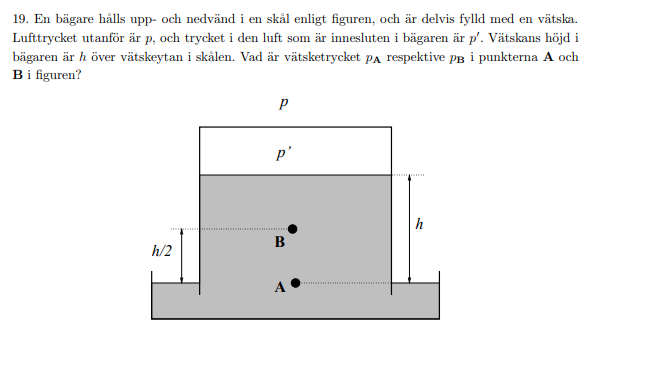
Det totala trycket i en punkt är summan av lufttrycket ovan för ytan och trycket från vätskepelaren. Dessutom gäller som du påpekar att det är samma tryck på samma höjd i ett kommunicerande kärl.
Det betyder att du kan ställa upp två uttryck för trycket i A (du har redan hittat ett!)
Kombinera det med ett uttryck för trycket i B.
Uppvärmning: Känner du till någon formel för att beräkna trycket i en vätska (eller trycket från en vätskepelare) på djupet ?
D4NIEL skrev:Det totala trycket i en punkt är summan av lufttrycket ovan för ytan och trycket från vätskepelaren. Dessutom gäller som du påpekar att det är samma tryck på samma höjd i ett kommunicerande kärl.
Det betyder att du kan ställa upp två uttryck för trycket i A (du har redan hittat ett!)
Kombinera det med ett uttryck för trycket i B.
Uppvärmning: Känner du till någon formel för att beräkna trycket i en vätska (eller trycket från en vätskepelare) på djupet ?
Ja! Så Pa=ρhg+p'=p och Pb=p'+ρ*(h/2)*g
Ja, och då kan du ju eliminera och få ett uttryck som bara innehåller och
(Observera att ditt slutliga svar inte får innehålla )
Eller enklare och snabbare: inse att trycket varierar linjärt med höjden.
D4NIEL skrev:Ja, och då kan du ju eliminera och få ett uttryck som bara innehåller och
(Observera att ditt slutliga svar inte får innehålla )
Ja tack! Jag insåg det till slut. Förresten, varför får inte svaret innehålla rå?
Svaret får i regel bara innehålla de variabler som finns i uppgiften om inget annat anges.
Vätskans densitet är en hjälpstorhet vi inför själva av bekvämlighet.
BTW, försök också förstå Pieters lösning, den är elegant och snabb :-)
D4NIEL skrev:Svaret får bara innehålla de variabler som finns i uppgiften om inget annat anges.
Vätskans densitet är en hjälpstorhet vi inför själva av bekvämlighet.
BTW, försök också förstå Pieters lösning, den elegant och snabb :-)
Ok, vad användbart att veta det då. Tack så jätte mycket för hjälpen. Ska försöka förstå Pieters lösning också :).
Pieter Kuiper skrev:Eller enklare och snabbare: inse att trycket varierar linjärt med höjden.
Är det för att trycket ges av ρHg? Då antar jag att höjden är x och trycket y. Men hur ska det hjälpa mig lösa frågan?
Colegate skrev:Pieter Kuiper skrev:Eller enklare och snabbare: inse att trycket varierar linjärt med höjden.
Är det för att trycket ges av ρHg? Då antar jag att höjden är x och trycket y. Men hur ska det hjälpa mig lösa frågan?
Om en storhet varierar linjärt med en parameter, hur stort är det då halvvägs när man vet värdet vid början och vid slutet?
Det har inget med x och y att göra, men det kanske hjälper att rita (på papper eller för sitt inre öga) en graf av storheten som funktion av parametern (i det här fallet trycket som funktion av höjd).
Pieter Kuiper skrev:Colegate skrev:Pieter Kuiper skrev:Eller enklare och snabbare: inse att trycket varierar linjärt med höjden.
Är det för att trycket ges av ρHg? Då antar jag att höjden är x och trycket y. Men hur ska det hjälpa mig lösa frågan?
Om en storhet varierar linjärt med en parameter, hur stort är det då halvvägs när man vet värdet vid början och vid slutet?
Det har inget med x och y att göra, men det kanske hjälper att rita (på papper eller för sitt inre öga) en graf av storheten som funktion av parametern (i det här fallet trycket som funktion av höjd).
Då tar du den värden på slutet + värden i början delat med två. Alltså (p+p')/2. Då förstår jag. Tack så mycket :).


