MaFy 2024 fråga 13
Vad är svaret på denna fråga?
Du kan ju lätt räkna ut något fall med numeriska värden.
Och/eller du kan använda uteslutningsmetoden.
Pieter Kuiper skrev:Du kan ju lätt räkna ut något fall med numeriska värden.
Och/eller du kan använda uteslutningsmetoden.
Är rätt svar B? Kan inte riktigt förklara varför jag tror de är B men försökte tänka med hjälp av denna klassikern: https://en.m.wikipedia.org/wiki/Monkey_and_hunter
marcusd74h skrev:Pieter Kuiper skrev:Du kan ju lätt räkna ut något fall med numeriska värden.
Och/eller du kan använda uteslutningsmetoden.Är rätt svar B?
Nej, avståndet borde öka för lång tid.
kan avståndet vara negativt?
RyanJ skrev:kan avståndet vara negativt?
Kan avståndet fortsätta minska efter att det har varit noll?
nej, då måste väl svaret vara A, eller?
RyanJ skrev:nej, då måste väl svaret vara A, eller?
Jag svarade c) men kan ha fel.
bollarna skulle ha olika lägen i början, då kan väl inte avståndet från början vara noll.
Jag tror svaret är A.
Men borde inte grafen vara spetsig?
RyanJ skrev:Men borde inte grafen vara spetsig?
Nej. Om de i början närmar sig varandra, finns det ett minsta avstånd smin, sedan ökar det igen.
Men det går som eller något.
RyanJ skrev:bollarna skulle ha olika lägen i början, då kan väl inte avståndet från början vara noll.
Där rök mina poäng...
Tänk dig att båda bollarna är på golvet av en hiss som faller fritt. En boll är stilla på golvet. En annan rullar rötlinjigt på golvet. Hur ändras avståndet över tid?
Ja. Det är så enkelt. När två kroppar faller utan luftmotstånd så ändras deras ykoordinater på samma sätt och de faller tillsammans så höjdkoordinaten är helt irrelevant.
Detta problem är sannolikt en referens till det klassiska kula-problemet där en kula avfyras horisontellt från ett gevär samtidigt som en identisk kula släpps brevid geväret. Newtons lagar säger då, något överaskande för vissa, att båda kulor träffar marken samtidigt.
SeriousCephalopod skrev:Tänk dig att båda bollarna är på golvet av en hiss som faller fritt. En boll är stilla på golvet. En annan rullar rötlinjigt på golvet. Hur ändras avståndet över tid?
Ja. Det är så enkelt. När två kroppar faller utan luftmotstånd så ändras deras ykoordinater på samma sätt och de faller tillsammans så höjdkoordinaten är helt irrelevant.
Detta problem är sannolikt en referens till det klassiska kula-problemet där en kula avfyras horisontellt från ett gevär samtidigt som en identisk kula släpps brevid geväret. Newtons lagar säger då, något överaskande för vissa, att båda kulor träffar marken samtidigt.
Och med det sagt, vilket är då svaret på frågan?
SeriousCephalopod skrev:Tänk dig att båda bollarna är på golvet av en hiss som faller fritt. En boll är stilla på golvet. En annan rullar rötlinjigt på golvet. Hur ändras avståndet över tid?
Ja. Det är så enkelt.
Och de behöver inte vara båda på golvet. Den stillastående kan sitta fast på en pinne eller ligga på en hög böcker.
Pieter Kuiper skrev:SeriousCephalopod skrev:Tänk dig att båda bollarna är på golvet av en hiss som faller fritt. En boll är stilla på golvet. En annan rullar rötlinjigt på golvet. Hur ändras avståndet över tid?
Ja. Det är så enkelt.
Och de behöver inte vara båda på golvet. Den stillastående kan sitta fast på en pinne eller ligga på en hög böcker.
Och med det sagt, vilket är svaret på frågan?
marcusd74h skrev:Pieter Kuiper skrev:SeriousCephalopod skrev:Tänk dig att båda bollarna är på golvet av en hiss som faller fritt. En boll är stilla på golvet. En annan rullar rötlinjigt på golvet. Hur ändras avståndet över tid?
Ja. Det är så enkelt.
Och de behöver inte vara båda på golvet. Den stillastående kan sitta fast på en pinne eller ligga på en hög böcker.
Och med det sagt, vilket är svaret på frågan?
A blir rätt svar. Tänk dig att bollarna alltid befinner sig på ett konstant y-avstånd (annars är ingen av följande grafer rimliga) medan x-avståndet är först (låt oss säga) 2 meter. Bollen med horisontell riktning kommer antingen närma sig den fallande bollen, eller åt andra hållet. OM bollen rör sig åt andra hållet så kommer avståndet mellan bollarna öka linjärt, men om bollarna rör sig mot en gemensam x-koordinatspunkt, så kommer det finnas ett läge där bollarna är på 0 meters avstånd i x-riktning, och det konstanta y-avståndet. Därefter ökar avståndet linjärt i all oändlighet (beroende på vart man nu släpper bollarna)
EDIT: Jag har i detta inlägg missat att ta med att gravitationen påverkar även bollen som rör sig i sidled. Se fortsatt diskussion längre ned i tråden.
Ett sätt att prova med en väldigt snabb (och inte särskilt vacker) skiss. De svarta märkena visar positionen för den fallande bilen, och de blå visar positionen för bollen som rör sig i sidled:
 Det viktiga här är att den svarta bollens hastighet ökar, medan den horisontella bollen rör sig med konstant hastighet.
Det viktiga här är att den svarta bollens hastighet ökar, medan den horisontella bollen rör sig med konstant hastighet.
Nu kikar vi på avståndet i varje ögonblick, genom att dra streck:
 I början är avståndet långt, sedan krymper det, och sedan ökar det igen. Det stämmer väl med alternativ A.
I början är avståndet långt, sedan krymper det, och sedan ökar det igen. Det stämmer väl med alternativ A.
Gör man en finare bild blir sambandet ännu tydligare, men detta räcker och går fort. :)
Pieter Kuiper skrev:Om de i början närmar sig varandra, finns det ett minsta avstånd smin, sedan ökar det igen.
Men det går som eller något.
Jag gav en formel, jag kan väl göra en plot också: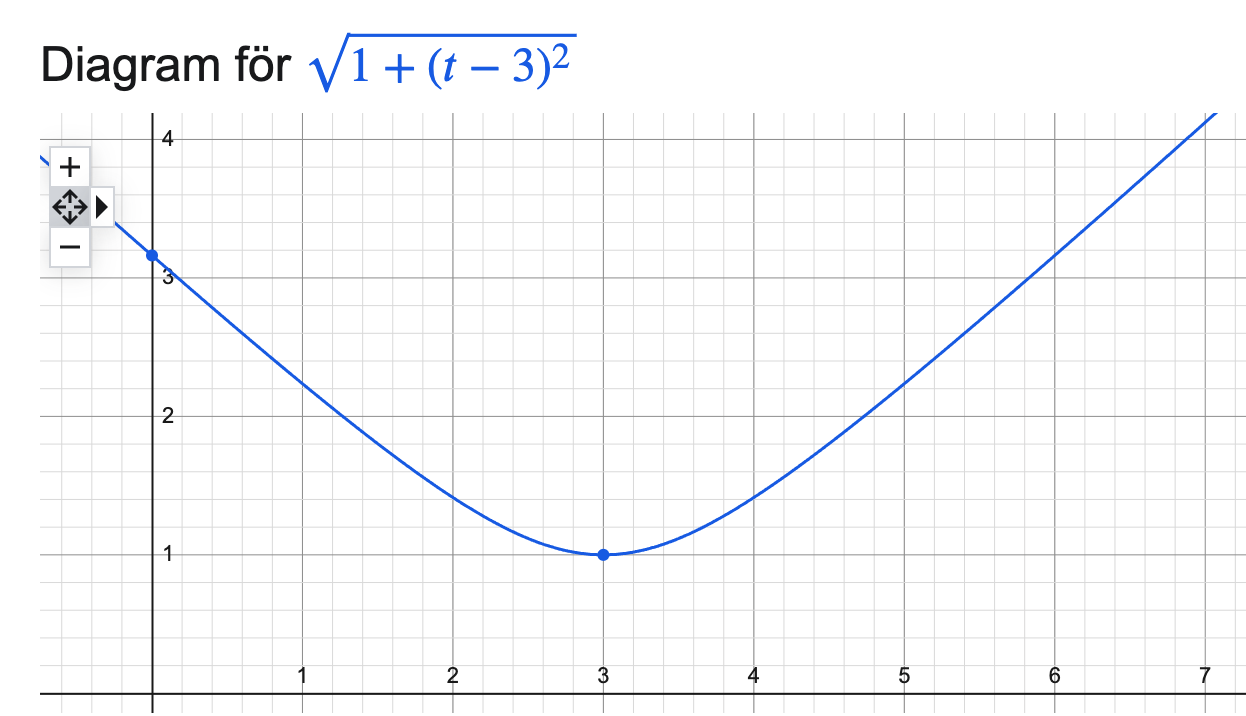
https://www.google.com/search?q=y=sqrt(1+(t-3)^2)
Och man ser att den blir spetsig om man zoomar ut.
Smutstvätt skrev:Det viktiga här är att den svarta bollens hastighet ökar, medan den horisontella bollen rör sig med konstant hastighet.
Båda bollars hastighet ökar eftersom båda faller.
Men om man själv faller med, ser man att den ena är i vila och att den andra åker förbi med en konstant hastighet.
Pieter Kuiper skrev:Smutstvätt skrev:Det viktiga här är att den svarta bollens hastighet ökar, medan den horisontella bollen rör sig med konstant hastighet.
Båda bollars hastighet ökar eftersom båda faller.
Men om man själv faller med, ser man att den ena är i vila och att den andra åker förbi med en konstant hastighet.
Sant, det missade jag. 😅
Pieter Kuipers knep är nog det bästa för att snabbt se hur avståndet förändras, men för den som inte kommer på det knepet, kommer här en uppdaterad skiss:

Avståndet i varje ögonblick (i rött):

Avståndet börjar hyfsat stort, krymper sedan, varpå det ökar igen.
Det går att hitta exempel där avståndet börjar som litet och sedan ökar (dvs. börjar i mitten av den v-formade kurvan som visas i alternativ A), men uppgiften efterfrågar inte om alla exempel, utan om ett möjligt exempel. Då faller C på att kulorna ska börja på olika ställen. D faller på att avståndet mellan kulorna inte kan vara negativt. Och B faller på att avståndet inte först kan öka mellan kulorna, och sedan minska igen (då måste någon av kulorna ha vänt i luften.




