mafy 2023 uppgift 6

Korra skrev:

Jag vet att sinx=cos(pi-x) och att cosx=sin(pi-x), ser inte hur det ska hjälpa. 

Hur ska jag tolka uppgiften? x (någon matematisk operation med okänt antal steg) y = sinx-cosx? Det kan stå vad som helst i kvadraten

Sin(pi/2-x) är en känd trigonometrisk samband. Samma sak med cos(pi/2-x) vilket du redan vet. Sen kan man ju använda subtraktionsreglerna /addition för sin o cos. Du kan använda den där sambandet för trig för de pi/2-x och sen additionregel för pi/2+x

Hur hjälper additionsreglerna? 

$\sin \left(\frac{\pi }{2}-x\right)=\cos x$
$\cos \left(\frac{\pi }{2}-x\right)=\sin x$
$\sin \left(\frac{\pi }{2}+x\right)=-\sin \left(-\frac{\pi }{2}-x\right)=-\sin \left(\frac{\mathrm{\pi }}{2}-x-\mathrm{\pi }\right)=\sin \left(\frac{\mathrm{\pi }}{2}-x\right)=\cos x$

$\cos \left(\frac{\mathrm{\pi }}{2}+x\right)=$… .

PATENTERAMERA skrev:

$\cos \left(\frac{\mathrm{\pi }}{2}+x\right)=$… .

= -sinx
Ser inte varför det ska hjälpa fortfarande. 
x (någonting) y ? = sinx-cosx

Istället för det konstiga tecknet så kan du använda funktionsnotation, om det är det konstiga tecknet som förvirrar. Dvs

x konstigt tecken y = f(x, y) = sinx - cosx.

Gäller det alltid att f((pi/2)-x, (pi/2)-x)=f(x, x)?

f((pi/2)-x, (pi/2)-x) = cosx - sinx.

f(x, x) = sinx - cosx.

Så (a) kan vi utesluta i alla fall.

Fortsätt med de andra.

Det svåra i denna uppgift är att man måste notera att

Det är inte helt självklart. Det är IMO dålig notation och borde skrivas

eller enl. HL ovan.

Vad är det för idiotisk uppgift. Jag kan också hitta på massa konstiga sätt att se på och lösa en matteuppgift, betyder det att personen som lyckas lösa är bättre på matte? Nej Irriterande

Om jag ser det som en funktion blir det ändå konstigt. Ta c) tillexempel 
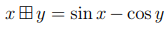Här ska jag alltså tänka: $\sin \left(\frac{\mathrm{\pi }}{2}+x\right)-\cos \left(\frac{\mathrm{\pi }}{2}+y\right)=-\cos y+\sin x$, om detta påståendet stämmer är det sant för alla värden x,y. ???

Nja, f(y, x) = siny - cosx, om f(x, y) = sinx - cosy.

Okej fine

Så nu tittar vi då på b)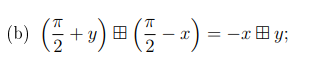
Då betyder detta alltså $\sin \left(\frac{\mathrm{\pi }}{2}+y\right)-\cos \left(\frac{\mathrm{\pi }}{2}-x\right)=-\sin x+\cos y$? Vet inte om denna likhet stämmer, men är det uppställt korrekt förutom likhetstecknet?

Det verkar stämma med likhetstecknet också, då är b rätt svar. Men har jag tänkt rätt?

pi/2 +y (ruta) pi/2 - x = sin(pi/2+y) - cos(pi/2-x) = cosy - sinx.

-(x (ruta) y) = -(sinx - cosy) = cosy -sinx.

Ja, det verkar stämma.

Tack så mycket