Mafy 2023 Uppgift 1
Uppgiften lyder:
1. En cirkelskiva kan snurra kring sin axel. Den påverkas av tre krafter enligt figuren. De tva krafterna med belopp F angriper på skivans periferi, och kraften med belopp G på en punkt på halva skivans radie. Vinkeln v är 30°. Vad är , om skivan är i jämvikt?
A. 0
B.
C.
D.

Jag har försökt att använda mig av vridmoment och jämviktsvillkoret för att lösa uppgiften. Men jag har fastnat och är osäker på hur jag ska gå vidare.
Här är mina försök hittills:
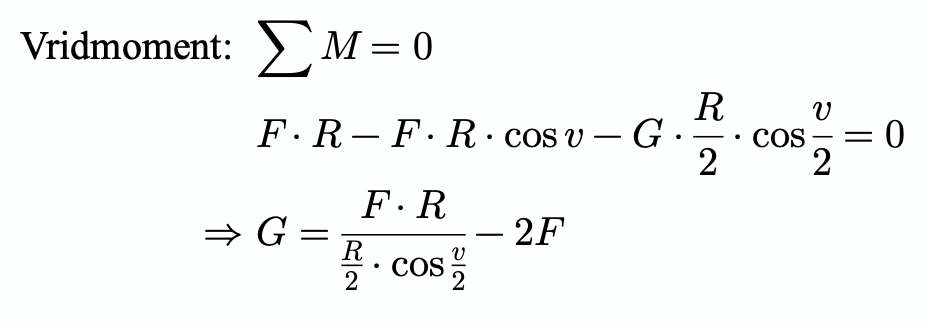
Jag är osäker på om min formel för vridmomentet stämmer och hur jag ska fortsätta för att lösa för . Skulle uppskatta om någon kunde hjälpa mig!
Tack på förhand!

Dani163 skrev:Jag är osäker på om min formel för vridmomentet stämmer
Motivera termerna i din formel.
(Men det går att välja rätt svar utan att skriva ner någon formel.)
Pieter Kuiper skrev:Dani163 skrev:Jag är osäker på om min formel för vridmomentet stämmer
(Men det går att välja rätt svar utan att skriva ner någon formel.)
Kan du visa?
Dani163 skrev:
Kan du visa?
Jag tror inte att mitt handwaving sätt att välja bland alternativen skulle tilltala dig, och det är också svårt för mig att skriva ner det på papper. Figur finns redan.
Jag undrade först och främst vad du har för formel där och hur du tänker.
Om du skriver ner hur du kom fram till dessa olika termer, kanske klarnar vissa saker redan där. I alla fall blir det enklare för oss att ge kommentarer.
Pieter Kuiper skrev:Dani163 skrev:
Kan du visa?Jag tror inte att mitt handwaving sätt att välja bland alternativen skulle tilltala dig, och det är också svårt för mig att skriva ner det på papper. Figur finns redan.
Jag undrade först och främst vad du har för formel där och hur du tänker.
Om du skriver ner det, kanske klarnar vissa saker redan där. I alla fall blir det enklare för oss att ge kommentarer.
I min formel för vridmoment har jag tagit hänsyn till de tre krafterna som verkar på cirkelskivan och deras momentarmar. För den första kraften, , som verkar på ytterkanten av skivan, är momentarmen enkel att bestämma eftersom den verkar på radien .
För den andra kraften, , som också verkar på ytterkanten av skivan, måste jag använda vinkeln för att räkna ut momentarmen. Eftersom kraften verkar i en vinkel mot horisontalplanet så påverkas inte hela radien av kraften, utan bara en del av den. Därför använder jag formeln för att räkna ut momentarmen.
För den tredje kraften, , som verkar i skivans tyngdpunkt, använder jag halva radien som momentarm.
Med vridmomentvillkoret utnyttjar jag att skivan är i jämvikt, vilket innebär att summan av alla vridmoment måste vara noll. Jag löser sedan ut från vridmomentvillkoret genom att räkna om formeln.
Dani163 skrev:
För den andra kraften, , som också verkar på ytterkanten av skivan, måste jag använda vinkeln för att räkna ut momentarmen. Eftersom kraften verkar i en vinkel mot horisontalplanet så påverkas inte hela radien av kraften, utan bara en del av den. Därför använder jag formeln för att räkna ut momentarmen.
Varför?
Jag kanske missar något men jag ser ingen skillnad mellan dessa två. Man kan vända på pappret eller vrida det. Och den vinkeln är väl inte inblandad där?
Pieter Kuiper skrev:Dani163 skrev:
För den andra kraften, , som också verkar på ytterkanten av skivan, måste jag använda vinkeln för att räkna ut momentarmen. Eftersom kraften verkar i en vinkel mot horisontalplanet så påverkas inte hela radien av kraften, utan bara en del av den. Därför använder jag formeln för att räkna ut momentarmen.Varför?
Jag kanske missar något men jag ser ingen skillnad mellan dessa två. Man kan vända på pappret eller vrida det. Och den vinkeln är väl inte inblandad där?
Jaha. Så är det tänkt då att för att räkna ut momentarmen för den andra kraften ska man använda istället? Eftersom kraften verkar i en vinkel mot horisontalplanet och påverkar inte hela radien , utan bara en del av den.
Tror inte det behövs att blanda in någon vinkel för krafterna med belopp F. Dem är väl parallella med varandra och båda vinkelräta mot radierna?
Dani163 skrev:
Eftersom kraften verkar i en vinkel mot horisontalplanet och påverkar inte hela radien , utan bara en del av den.
Du kanske misstolkar figuren. Något horisontalplan finns inte specificerat i uppgiften och det spelar ingen roll om axeln är vertikal eller horisontal. Uppgiften ska säkert tolkas som om det handlade om samma geometri som av ett cykelhjul.
Jag kan inte tolka vad du menar med "påverkar inte hela radien".
Jag löste uppgiften såhär:
Vi kan säga att summan av momenten = 0. Det finns 3 krafter på skivan. Sedan måste vi ta hänsyn till teckenkonventionen baserat på rotationsriktningen. Två krafter F kommer att rotera skivan i samma riktning och kommer att rotera den i en annan riktning. Netto-momentet blir då . Då skivan är i jämvikt betyder det att skivan inte roterar, alltså är nettomomentet 0.
Vi sätter in de kända värdena i ekvationen och isolerar G. Vinkeln mellan r och F är 90, vinkeln mellan r och G är 30, nettomomentet är 0.
Nettomomentet blir då , vi isolerar G och får . Sedan får vi , , och slutligen .
Dani163 skrev:
Netto-momentet blir då .
Jag förstår inte varför du skriver så.
Ur resten blir tydligt att samma beteckning används där för helt olika vinklar.
Pieter Kuiper skrev:Dani163 skrev:
Netto-momentet blir då .Jag förstår inte varför du skriver så.
Ur resten blir tydligt att samma beteckning används där för helt olika vinklar.
Två av dessa har vinkeln 90, en har vinkeln 30. sin(90) = 1, så jag förenklar bara till rF på båda.
Dani163 skrev:Två av dessa har vinkeln 90, en har vinkeln 30.
Men skriv inte så. Det leder bara till oreda.
Om man använder formler och ekvationer för att lösa det här, då ska det göras på ett korrekt sätt.
Pieter Kuiper skrev:Om man använder formler och ekvationer för att lösa det här, då ska det göras på ett korrekt sätt.
Okej, man gör misstag, varför göra en höna av en fjäder?
Dani163 skrev:Pieter Kuiper skrev:Om man använder formler och ekvationer för att lösa det här, då ska det göras på ett korrekt sätt.
Okej, man gör misstag, varför göra en höna av en fjäder?
Kanske för att försöka hjälpa dig?
Pieter Kuiper skrev:Dani163 skrev:Pieter Kuiper skrev:Om man använder formler och ekvationer för att lösa det här, då ska det göras på ett korrekt sätt.
Okej, man gör misstag, varför göra en höna av en fjäder?
Kanske för att försöka hjälpa dig?
Ja för dina en-mening svar hjälper otroligt mycket!
Behövde kolla med någon annan för att komma fram till rätt svar. Tack ändå!


