mafy 2022 liknande uppgift till uppgift 7

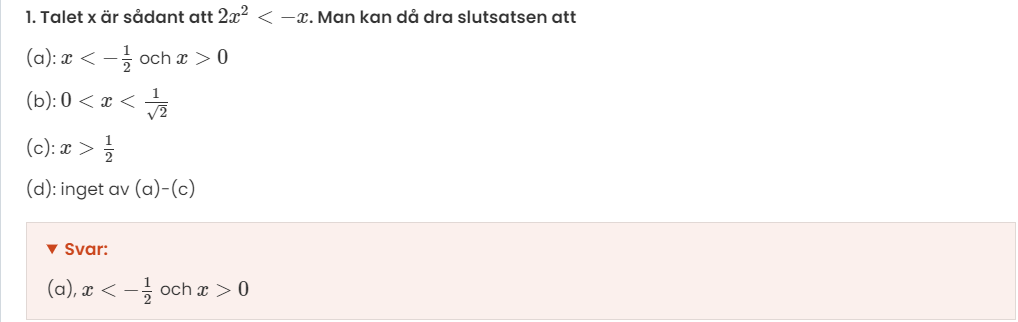
Hej! Jag förstår inte riktigt varför det blir svaret a). Jag förde över alla x till vänster led så att VL<0 och därefter faktorisera ut x. Därefter testade jag med x=-2 som är mindre än -1/2 vilket gav att vänster led blev 6 medans högerled är 0 alltså 6>0 vilket gör att a borde väl inte stämma då det måste vara att VL<0?

Blir det a)?

Endast i (-1/2,0) är parabeln under den räta linjen.

Däremot om frågan hade varit 2x^2 > -x....

Hur skulle jag kunna lösa denna fråga algebraiskt?

Det verkar som att någon klantig uppgiftskonstruktör har vänt på olikheten... 😅

Algebraisk lösning:

Faktorisering ger att

$2 x^{2} + x < 0 x (2 x + 1) < 0$

Här kan ett teckenschema vara användbart:

		-1/2		0
x	-	-	-	0	+
2x+1	-	0	+	+	+
x(2x+1)	+	0	-	0	+

Så som Trinity2 säger, svaret på uppgiften som den är formulerad just nu är (d).

Haha, det är ingen fara. Lösningsförslagen överlag är toppen. Hur tog du fram minus/plus tecknen samt 0? Har inte använt teckenschema förut.

Tillägg: 8 maj 2024 21:15

Nvm, förstod hur man gjorde efter några tester. Tack för svaren!

calmfrenzy skrev:
Haha, det är ingen fara. Lösningsförslagen överlag är toppen.

Från mig och ConnyN, tack! 😊

Hur tog du fram minus/plus tecknen samt 0? Har inte använt teckenschema förut.

Teckenscheman används för att ta reda på när en faktor byter tecken. Gör en tabell med rader för varje faktor, samt för produkten/kvoten/sammanställningen generellt. För respektive faktor noterar du för vilket värde de byter tecken.

x byter tecken vid noll
2x+1 byter tecken vid -1/2

Gör en kolumn för varje sådant teckenbyte, samt en kolumn emellan varje. I detta exempel blir det fem kolumner (utöver kolumnen med faktorerna, längst till vänster):

	<-1/2	-1/2	-1/2<x<0	0	0<x
x
2x+1
x(2x+1)

Nu fyller vi i vilket värde respektive faktor har för varje värde/intervall (fetstilt). Därefter beräknas produkten för respektive intervall (kursivt).

	<-1/2	-1/2	-1/2<x<0	0	0<x
x	-	-	-	0	+
2x+1	-	0	+	+	+
x(2x+1)	+	0	-	0	+

Det är magin! Det går att göra samma sak för att bestämma tecken för bråk och liknande. :)

calmfrenzy skrev:

Tillägg: 8 maj 2024 21:15

Nvm, förstod hur man gjorde efter några tester. Tack för svaren!

Attans, han skriva en förklaring 😅. Men men, det kan alltid vara till nytta för någon annan. :)

Åh nej, förlåt. Men det hjälper ändå då jag hade bara en övergripande förståelse för hur det går till. Så tack!

Du behöver absolut inte be om ursäkt! :)

Välkommen till Pluggakuten förresten! :)

Tack! Glad att vara här. Har tagit mycket hjälp tidigare, tänkte det är väl lika bra att gå med. :D

Kul att höra! :)

Svara Avbryt

Visa senaste svar