Mafy 2019 Uppgift 29

Hej!

Jag skulle uppskatta lite hjälp med att lösa följande uppgift:

"29. Vinkeln vid hörnet $C$ i triangeln $ABC$ är trubbig. Givet att $|BC|=a$ , $|CA|=b$ (längdenheter), och triangelns area är $S$ (areaenheter), beräkna och ange längden av sidan $AB$ , uttryckt i termer av $a, b$ och $S$ ."

Jag har försökt att lösa uppgiften genom att rita en figur och använda pytagoras sats. Men jag har stött på problem och undrar om någon kan hjälpa mig.

Jag har tagit hjälp av någon på nätet som ritade figuren åt mig och föreslagit att vi lägger till två sidor, $x$ och $y$ , för att få en rätvinklig triangel med sidorna $y$ , $(x+b)$ och $AB$ . De ekvationer som de ställde upp såg ut på följande vis:

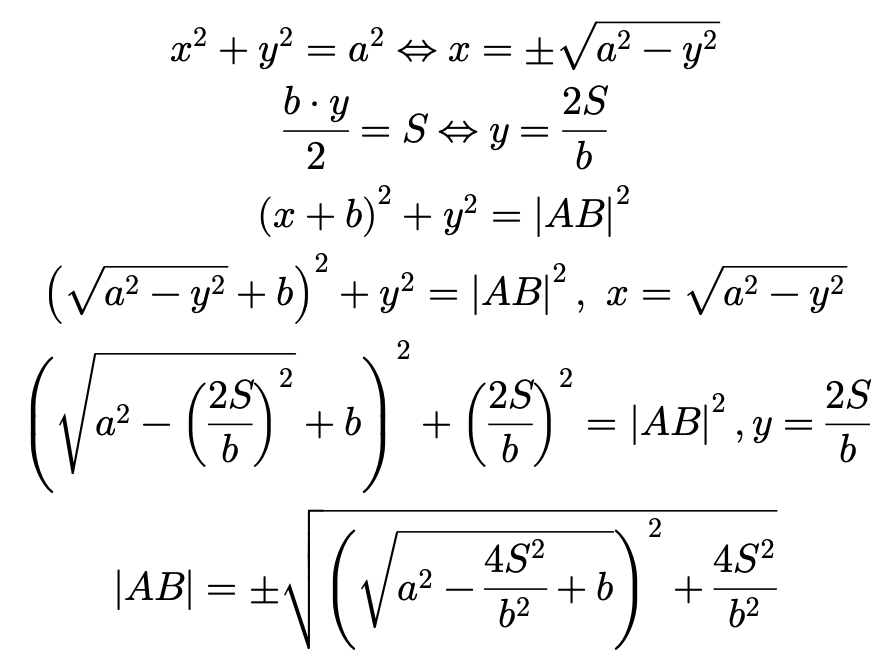
Men jag blir inte klokare. Så vad är lättaste metoden att lösa den på? Vilken information kan vi använda för att lösa ut $AB$ i termer av $a$ , $b$ och $S$ ?

Tack på förhand!

Den här sidan kan säkert ge något.

Bedinsis skrev:
Den här sidan kan säkert ge något.

$S = \frac{ab \sin(C)}{2}$
Jag förstår att det är så vi får S, men inte sen hur den kommer in i bilden för att få ut sidan AB. Tänker du då cosinussatsen?

$c^2 = a^2 + b^2 - 2ab\cos(C).$

Sen att man uttrycker cos(C) i termer av sin(C) för att substituera in formeln för areasatsen? Den är $\sin(C) = \sqrt{1-cos^2(C)}$ .

Det låter som en god idé. Pröva.

Bedinsis skrev:
Det låter som en god idé. Pröva.

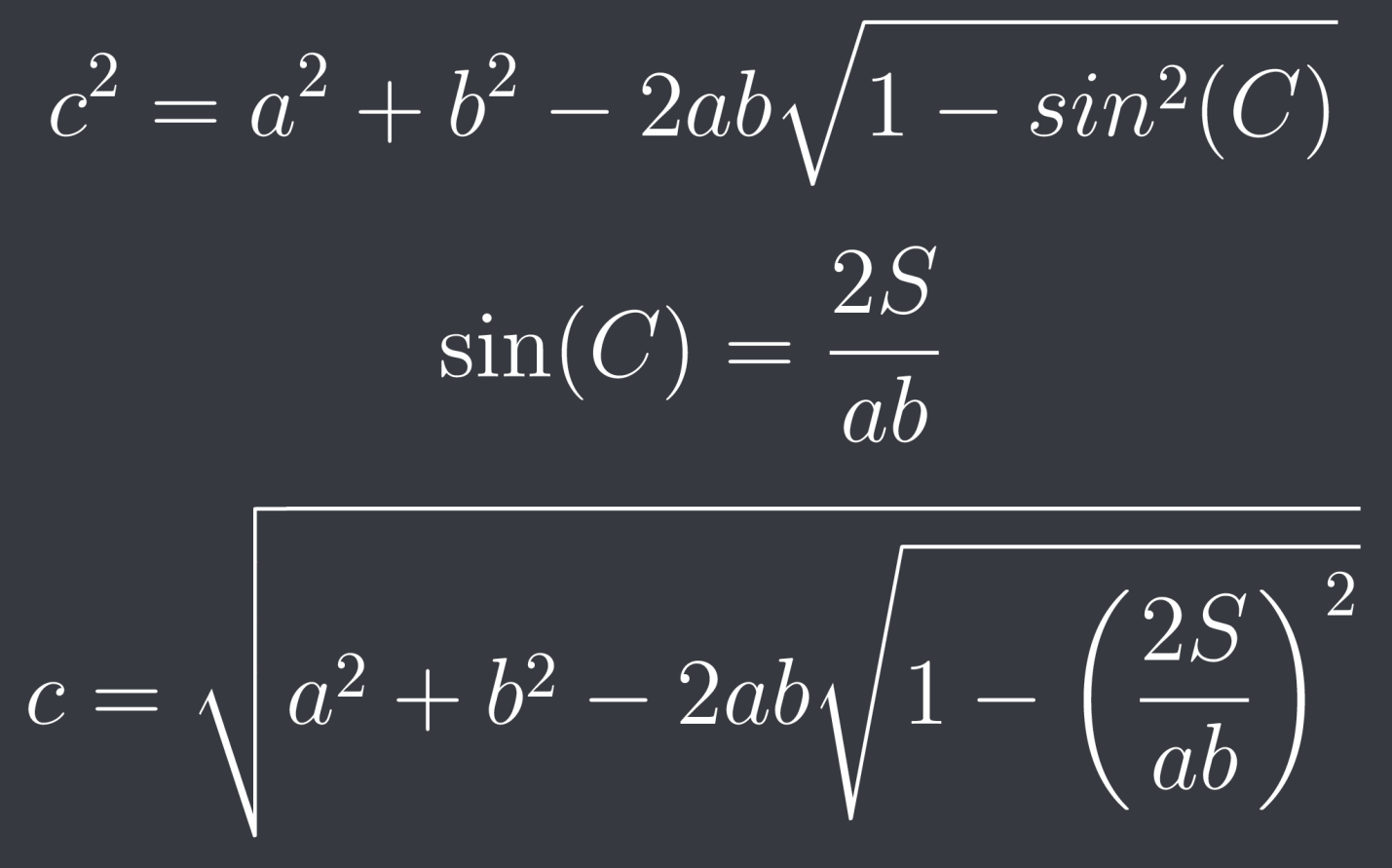
Hur gör man härifrån sen, skulle det räcka att svara så eller behöver det förenklas ännu mer?

c = AB.

Tänk på att C är en trubbig vinkel, vilket betyder att cos(C)<0, alltså cos(C)= - $\sqrt{1 - \sin^{2} (C)}$ .

Mohammad Abdalla skrev:
Tänk på att C är en trubbig vinkel, vilket betyder att cos(C)<0, alltså cos(C)= - $\sqrt{1 - \sin^{2} (C)}$ .

Ah fattar. Blir det då såhär istället?

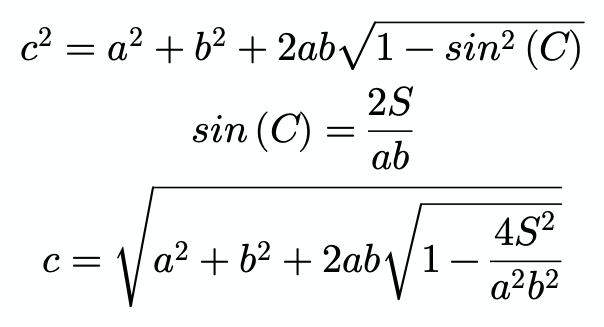
Sen om man kan förenkla det ännu mer vet jag inte.

Svara

Visa senaste svar