Mafy 2019 uppgift 19

Hej!
Jag tänker mig en rektangel uppfyller inte b) men sen finns det parallellogram och kvadrat där parallellogram uppfyller a) men ej de andra alternativ och en kvadrat är jag osäker över om den uppfyller c) för jag tror ej den uppfyller b). Jag kan ej låta bli att svara d) här eftersom de andra fyrhörningar som då är specialfall av romb fyller ej alltid alla alternativ. Det kanske finns lättare sätt att närma sig denna uppgift än vad jag gjorde
Jag kan inte följa logiken i det du skriver.
Jag väljer något annat än d. Prova att göra en fyrhörning som uppfyller a och inte är en romb. Gör sedan en som är en romb.
Och gör samma saker med b och c.
Vad menar du med "fyller ej alltid alla alternativ"? Alla a-c ska inte vara uppfyllda. Bara en av dem, eller ingen alls.
Laguna skrev:Jag kan inte följa logiken i det du skriver.
Jag väljer något annat än d. Prova att göra en fyrhörning som uppfyller a och inte är en romb. Gör sedan en som är en romb.
Och gör samma saker med b och c.
Vad menar du med "fyller ej alltid alla alternativ"? Alla a-c ska inte vara uppfyllda. Bara en av dem, eller ingen alls.
Hm det enda jag kan komma på som uppfyller a) är en kvadrat, rektangel och parallellogram.
b) är det mest romb jag tänker på men rektangel,kvadrat och parallellogram uppfyller ej den.
c) är det bara rektangel som uppfyller och kvadrat kanske(osäker) men ej romb eller parallellogram.
Det är såhär jag menar att jag gjorde det
För att förtydliga frågan:
Är det något av villkoren a, b eller c som bara gäller för en romb och inte för andra fyrhörningar?
Ture skrev:För att förtydliga frågan:
Är det något av villkoren a, b eller c som bara gäller för en romb och inte för andra fyrhörningar?
Vad jag vet om en romb är alla sidor lika stor och motstående vinklar är lika stora/diagonaler har bisektris till vinklar vid hörnen. a) gäller som sagt för rektanglar,kvadrat och parallellogram. b) gäller för ej för dem utan bara en romb. c) är jag osäker på om det gäller för rektanglar ,men jag är säker på att den gäller för en kvadrat då alla sidor är lika stora som en romb , men för en parallellogram och en rektangel är jag osäker på om c) kan uppfylla det.
Fyrhörningar kan se ut på alla möjliga sätt, det dom har gemensamt är att de har fyra sidor. Sidorna behöver inte vara parvis lika, de är ändå fyrhörningar, så länge de har fyra hörn. (Och sidor)
Men är det någon av egenskaperna a till c som bara gäller för romber?
Ture skrev:Fyrhörningar kan se ut på alla möjliga sätt, det dom har gemensamt är att de har fyra sidor. Sidorna behöver inte vara parvis lika, de är ändå fyrhörningar, så länge de har fyra hörn. (Och sidor)
Men är det någon av egenskaperna a till c som bara gäller för romber?
Ah okej jo men det är sant. Jag tänker a-c gäller för en romb. Det är egenskaper hos en romb. Jag tänker b) är bara typisk för romber för jag har aldrig hört att andra fyrhörningars diagonaler bildar rät vinkel. b) borde vara rätt svar tänker man men det är det ej..
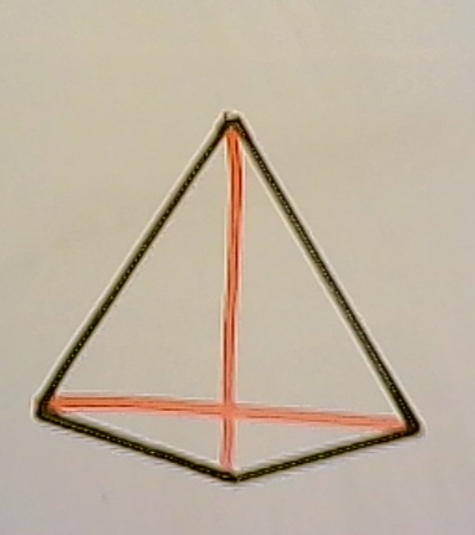
Här är en fyrhörning som inte är en romb, men ändå har vinkelräta diagonaler

Ture skrev:Här är en fyrhörning som inte är en romb, men ändå har vinkelräta diagonaler
Okej det var bra att komma på den. Då är det ej bara en romb. Här delar ej diagonalerna varandra mitt itu som andra fyhörningar kan göra tex kvadrat,rektangel och parallellogram.
Nu tror jag att du är med på att alla villkoren a,b och c gäller för romber, frågan är:
Är det något av villkoren som bara gäller för romber, och inga andra fyrhörningar?
Du skrev i #3 att villkor a även gäller för rektanglar, då kan vi stryka det villkoret.
I inlägg #8 ser vi ett exempel på en figur som uppfyller villkor b utan att vara en romb. Då kan vi stryka b.
Återstår villkor c, finns det någon annan typ av fyrhörning än en romb som uppfyller det villkoret?
Ture skrev:Nu tror jag att du är med på att alla villkoren a,b och c gäller för romber, frågan är:
Är det något av villkoren som bara gäller för romber, och inga andra fyrhörningar?
Du skrev i #3 att villkor a även gäller för rektanglar, då kan vi stryka det villkoret.
I inlägg #8 ser vi ett exempel på en figur som uppfyller villkor b utan att vara en romb. Då kan vi stryka b.
Återstår villkor c, finns det någon annan typ av fyrhörning än en romb som uppfyller det villkoret?
jaha så man behöver bara visa en enda fyrhörning som uppfyller villkoren ? Ja jag sa att villkor a) gäller för rektanglar men även kvadrat och parallellogram.
villkor c) är jag osäker om det finns fyrhörningar som uppfyller det. Kvadrat kanske likt romber?