Mafy 2019 del C
Hej!
Hur kan man lösa denna fråga utan linjär algebra kunskaper?

Pröva att rita både linjen och punkterna i x/y-planet.
Försök att hitta något geometriskt samband i din skiss.
Visa hur långt du kommer.
Tänk på att det finns två fall, antingen ligger punkterna på samma sida om linjen, eller på olika sidor om linjen.
D4NIEL skrev:Tänk på att det finns två fall, antingen ligger punkterna på samma sida om linjen, eller på olika sidor om linjen.
Hm så man skall göra två beräkningar för dessa två fall?
Om man nu gör på linjär algebra sättet så kan jag tänka mig så

Det ser ut som om du ritat punkterna A och B på linjen l ?! Så står det inte i uppgiften.
farfarMats skrev:Det ser ut som om du ritat punkterna A och B på linjen l ?! Så står det inte i uppgiften.
De säger ju att punkterna A och B är i planet så då ska den ligga där eller? 
Yngve skrev:Pröva att rita både linjen och punkterna i x/y-planet.
Försök att hitta något geometriskt samband i din skiss.
Visa hur långt du kommer.

Eftersom det bara handlar om ett enda plan så kan du betrakta ditt papper som det planet.
I din senaste bild ligger A och B fortfarande på linjen. Det står i uppgiften att de har vissa avstånd till linjen.
Laguna skrev:Eftersom det bara handlar om ett enda plan så kan du betrakta ditt papper som det planet.
I din senaste bild ligger A och B fortfarande på linjen. Det står i uppgiften att de har vissa avstånd till linjen.
Om du syftar på att bild #7 är felaktig så kan jag sudda den?
Här är en annan bild där punkterna ej ligger på linjen.

Ok, nu ligger de utanför linjen, kan du markera de vinkelräta avstånden?
D4NIEL skrev:I alla bilder du ritat hittills ligger dina punkter på linjen.
Men man ska kunna mäta ett avstånd mellan varje punkt och linjen. Punkterna får alltså inte ligga på linjen.
Ja jag vet. Men i inlägg #9 är det ej det. Ser det rätt ut? Jag förstår ej hur avståndet från punkt A till L samt punkt B till L blir vinkelrät? Jag läste bara av avståndet i uppgiften och tolkade ej som att något avstånd är vinkelrät.
D4NIEL skrev:Ok, nu ligger de utanför linjen, kan du markera de vinkelräta avstånden?

När man pratar om ett avstånd till en linje menar man det vinkelräta avståndet. Här har jag ritat in hjälplinjer för att det ska vara enklare att se de vinkelräta avstånden. Den tjocka linjen är "linjen". Kan du sätta in måtten enligt uppgiften och se om du kan räkna ut den ortogonala projektionen? Kom också ihåg att du har ett fall till, nämligen det då punkterna ligger på olika sidor om linjen.

D4NIEL skrev:När man pratar om ett avstånd till en linje menar man det vinkelräta avståndet. Här har jag ritat in hjälplinjer för att det ska vara enklare att se de vinkelräta avstånden. Den tjocka linjen är "linjen". Kan du sätta in måtten enligt uppgiften och se om du kan räkna ut den ortogonala projektionen? Kom också ihåg att du har ett fall till, nämligen det då punkterna ligger på olika sidor om linjen.
Jag har glömt hur man gjorde ortogonal projektion och tänker typ om man kan hålla sig till hur man hade räknat om man ej vet vad orotogonal projektion innebär. Vi kan se i min nya bild att A har vinkelrät avstånd till linjen och jag försökte göra likadant med punkten B. Hur översätter man ortogonalprojektion av AB på L begreppet till gymnasienivå?

Avstånd mellan en punkt och en linje är det kortaste avståndet, och det är alltid vinkelrätt mot linjen. I din bild är avståndet från A inte vinkelrätt mot linjen L! Däremot är avståndet från B i din figur nästan vinkelrätt mot linjen L
Se bilden nedan, där l är linjen och den streckade linjen symboliserar avståndet mellan linjen l och punkten A

på samma sätt kan vi rita in en punkt B och markera det vinkelräta avståndet

Ture skrev:Avstånd mellan en punkt och en linje är det kortaste avståndet, och det är alltid vinkelrätt mot linjen. I din bild är avståndet från A inte vinkelrätt mot linjen L! Däremot är avståndet från B i din figur nästan vinkelrätt mot linjen L
Se bilden nedan, där l är linjen och den streckade linjen symboliserar avståndet mellan linjen l och punkten A
på samma sätt kan vi rita in en punkt B och markera det vinkelräta avståndet
Aa okej men det låter logiskt. Då får vi en en rektangel och triangel.
Jag vet ej om man får göra såhär. Vad är det vi ska räkna ut?

Nu ser allt bra ut. Vad blir x?
destiny99 skrev:
Jag vet ej om man får göra såhär. Vad är det vi ska räkna ut?
Det är x som är den ortogonala (vinkelräta) projektionen av sträckan AB på linjen L
Om du tänker dig att du belyser sträckan AB med parallellt ljus som är vinkelrätt mot linjen L kommer den ortogonala projektionen på L att vara skuggan från sträckan AB
Laguna skrev:Nu ser allt bra ut. Vad blir x?
16
visst,
men som D4NIELskrev i inlägg #3, så finns det ett fall till som du måste beräkna!
Ture skrev:visst,
men som D4NIELskrev i inlägg #3, så finns det ett fall till som du måste beräkna!
Ja det fallet har jag lite svårt för..
Ture skrev:Rita!
"Om du tänker dig att du belyser sträckan AB med parallellt ljus som är vinkelrätt mot linjen L kommer den ortogonala projektionen på L att vara skuggan från sträckan AB"
Jag förstår ej detta. Vill du förtydliga detta? X är parallell med linjen och ej vinkelrät ?
Ture skrev:Rita!

Snyggt!
Fortsätt på samma sätt som tidigare.
Det är fortfarande Pythagoras sats som gäller, men med ett annat mått på ena kateten.
destiny99 skrev:
"Om du tänker dig att du belyser sträckan AB med parallellt ljus som är vinkelrätt mot linjen L kommer den ortogonala projektionen på L att vara skuggan från sträckan AB"
Jag förstår ej detta. Vill du förtydliga detta? X är parallell med linjen och ej vinkelrät ?
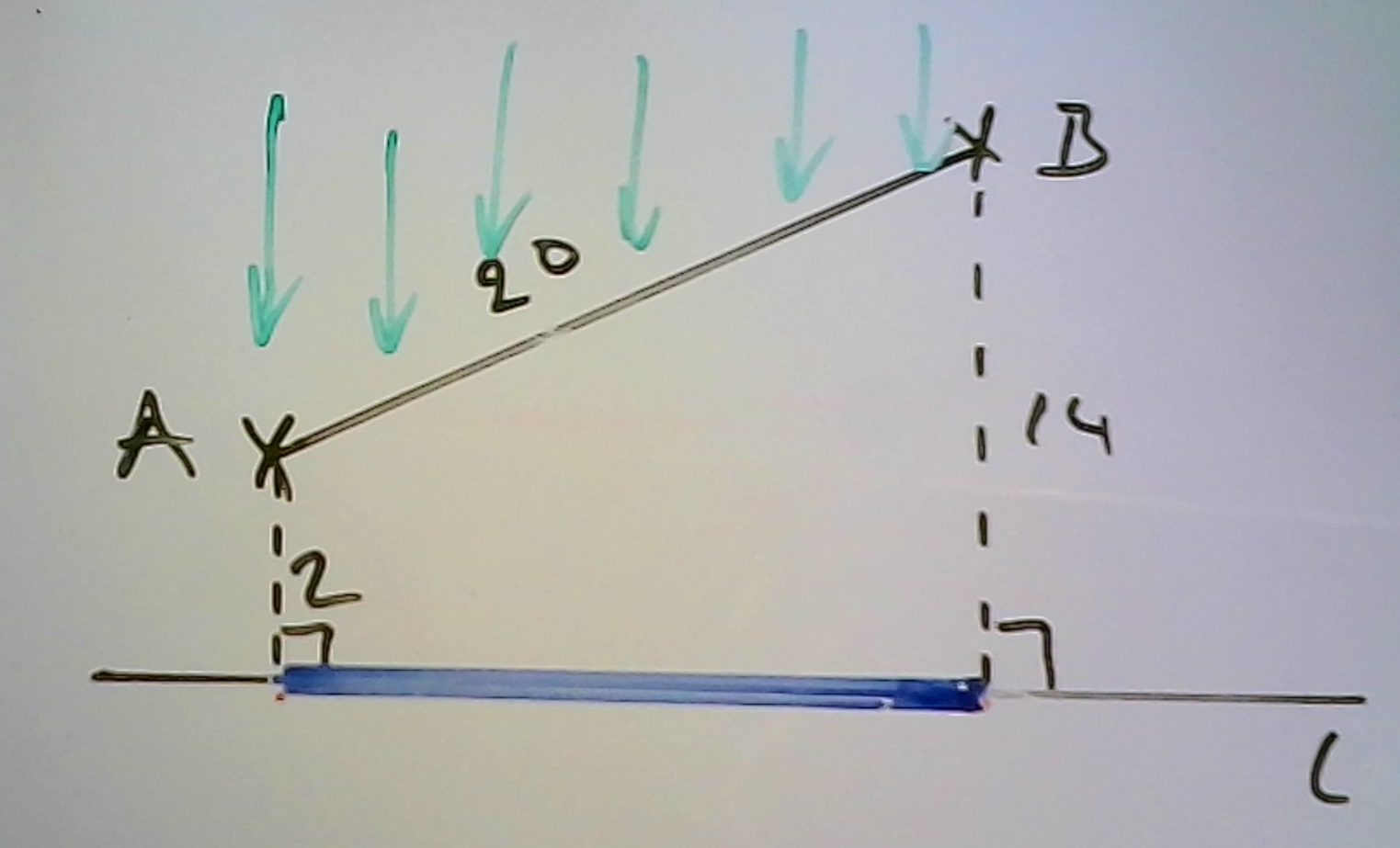
På bilden nedan är de gröna pilarna ljus som infaller vinkelrätt mot linjen L
Det blå området ska symbolisera den skugga som uppstår från Linjen AB (vi kan tänka oss att linjen har en tjocklek )
Skuggan är den ortogonala projektionen av sträckan AB på linjen L och det är den som du har beräknat till 16.
Ture skrev:destiny99 skrev:
"Om du tänker dig att du belyser sträckan AB med parallellt ljus som är vinkelrätt mot linjen L kommer den ortogonala projektionen på L att vara skuggan från sträckan AB"
Jag förstår ej detta. Vill du förtydliga detta? X är parallell med linjen och ej vinkelrät ?
På bilden nedan är de gröna pilarna ljus som infaller vinkelrätt mot linjen L
Det blå området ska symbolisera den skugga som uppstår från Linjen AB (vi kan tänka oss att linjen har en tjocklek )
Skuggan är den ortogonala projektionen av sträckan AB på linjen L och det är den som du har beräknat till 16.
Men den horisontella sträckan från punkten A som går vinkelrät mot avståndet BL är alltså den ortogonala projektionen (skuggan)?
Yngve skrev:Snyggt!
Fortsätt på samma sätt som tidigare.
Det är fortfarande Pythagoras sats som gäller, men med ett annat mått på ena kateten.
Jag fick nu 12 l.e. dock är jag ej med på varför vi behövde räkna y på det sättet också som vi borde med x.

destiny99 skrev:
Jag fick nu 12 l.e. dock är jag ej med på varför vi behövde räkna y på det sättet också som vi borde med x.
Du kan kalla sträckan längs med linjen L för x även i det här fallet.
Du kan gärna läsa denna beskrivning av en projektion i det tredimensionella fallet. Den använder vektorer som kanske ger bättre förståelse.






