MAFY 2018 Uppgift 18
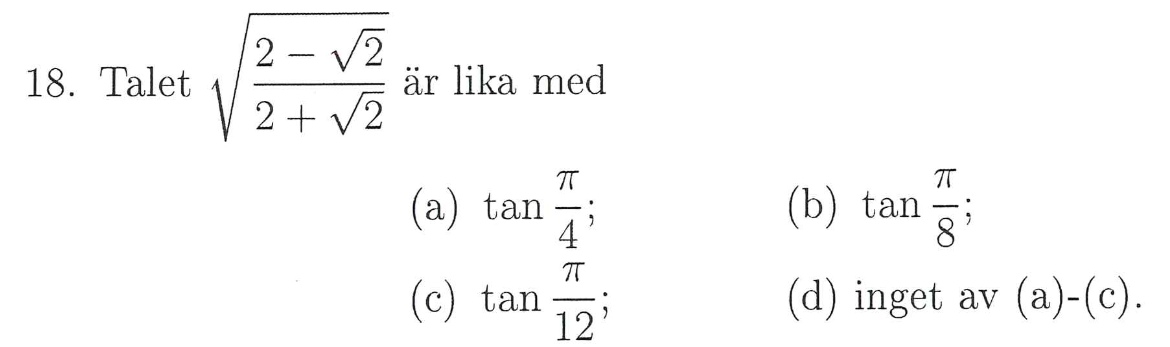
Alternativ a är lätt att räkna ut, den visar sig vara fel så jag stryker den omedelbart. Men hur ska jag kolla vilket av de andra alterantiven som stämmer? Finns det något smidig metod att tillämpa?
Svar enligt facit: b
Ser inget uppenbart enkelt sätt.
Kvadrera och använd att
Skriv om HL uttryckt i cos(2v). Sedan kan du testa v = pi/8 eller pi/12 med kända värden på cos(pi/4) och cos(pi/6).
Dr. G skrev:Ser inget uppenbart enkelt sätt.
Kvadrera och använd att
Skriv om HL uttryckt i cos(2v). Sedan kan du testa v = pi/8 eller pi/12 med kända värden på cos(pi/4) och cos(pi/6).
Hur kan jag skriva om HL uttryckt i cos(2v) ? Jag vet att cos(2v) =
Sedan då?
så
Dr. G skrev:så
Nu har jag förstått. Tack för hjälpen!
Jag blir faktiskt imponerad, och nyfiken vad ni som hjälper på pluggakuten jobbar med. Hur kan ni komma på saker och ting så snabbt? Jag tror inte min lärare hade listat ut svaret lika snabbt som du gjorde Dr. G
När det gäller trigonometri så hjälper ofta omskrivningar. (Ibland går det fort och ibland inte så fort.)
Med trigonometriska ettan och formlerna för dubbla vinkeln (framlänges eller baklänges) så kommer man ofta ganska långt. Om man vet vilka verktyg man har i lådan så kan man prova något som verkar ta en i rätt riktning.
Om man kommer ihåg eller härleder dubbla vinkeln för tangens så går den lika bra här.
HL kan räknas ut med det givna värdet på tan(v) till 1, vilket ger att VL = tan(2v) = 1, så t.ex 2v = pi/4.


