mafy 2017 uppg 23
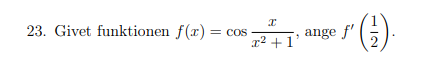
Hej, hur går man tillväga för lösa en sådan uppgift? Jag vet inte ens hur man ska börja...
Jag skulle börja med att identifiera vilka funktioner som ingår. Vi har en yttre funktion, och en inre funktion, . De två är sammansatta till funktionen . Derivatan av en sammansatt funktion är .
Ta fram derivatorna g'(x) och h'(x). Sedan sätter du ihop allt. :)
EDIT: Korrigerat derivatan till kedjeregeln.
Smutstvätt skrev:Jag skulle börja med att identifiera vilka funktioner som ingår. Vi har en yttre funktion, och en inre funktion, . De två är sammansatta till funktionen . Derivatan av en sammansatt funktion är .
Ta fram derivatorna g'(x) och h'(x). Sedan sätter du ihop allt. :)
Det där ser ut som produktregeln.
Suck, ja det har du helt rätt i. 😞 Någon här är trött.
Jag har tagit fram derivatan för både g(x) och h(x) men vet dock inte hur jag går vidare för att ta fram D(g(h(x))). g'(h(x)) är problemet...
calmfrenzy skrev:Jag har tagit fram derivatan för både g(x) och h(x) men vet dock inte hur jag går vidare för att ta fram D(g(h(x))). g'(h(x)) är problemet...
D [ f(g(x)) ] = f'(g(x)) * g'(x).
Börja med att beräkna
f'
g'
och sätt sedan samman byggstenarna.
Nuså nu funkar det, förståd inte hur man skulle räkna ut f'(g(x)) till en början men kom fram till att f'(g(x)) betydde med andra ord -sin(x/(x^2+1)) där -sin=f' och g(x)=x/(x^2+1). Tack för hjälpen!


