Maclaurinutvecklingar

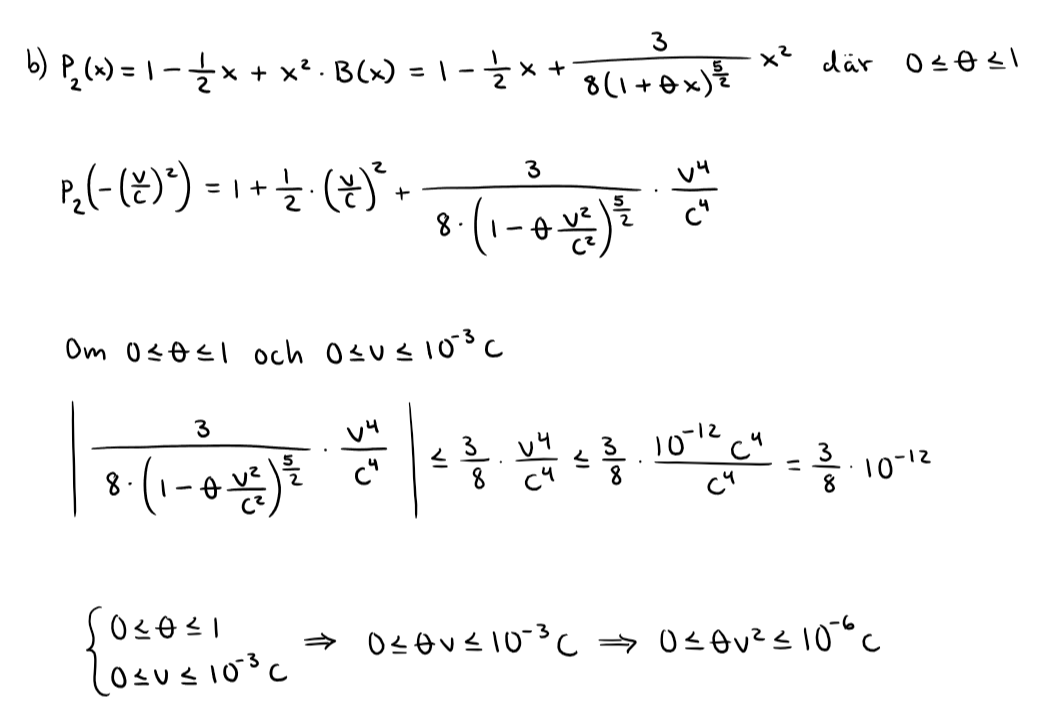
Vad fick du på a) egentligen? Utvecklingen (i fyra termer) borde bli

$T(v)=\frac{m_0 v^2}{2}+\frac{3 m_0 v^4}{8 c^2}+O\left(v^5\right)$

Approximationen vi brukar använda är såklart $\displaystyle \frac{m_0v^2}{2}$, dvs den kinetiska energin vi känner igen från gymnasiefysiken.

Nu kan  du använda "fjärdegradstermen" som feluppskattning / Restterm. Eftersom den är strängt växande kommer maxvärdet uppstå då $v=v_{max}$, dvs $v=10^{-3}c$

Dela alltså resttermen med approximationen och sätt sedan in maxvärdet på $v$ (dvs $\theta=1$ om du använder en sådan uppställning), visa att talet du får är mindre än $10^{-6}$

Jag fattar inte riktigt vad du menar. Jag satt in v = 10^(-3)*c men då blir det också fel

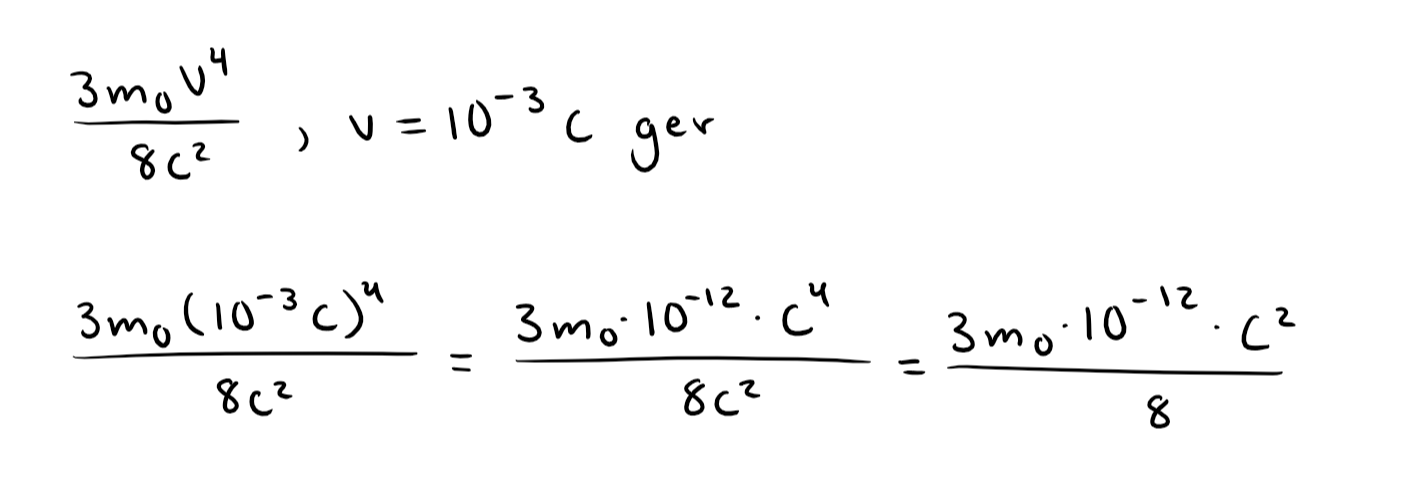
Jag får en känsla av att du inte är med på vad vi gör från början (även om du kan dela det du fått fram med approximationen och på så visa att du ligger inom felmarginalen).

Låt oss istället ta det från början, serieutvecklingen av $T(v)$ blir

$T(v)=T(0)+\frac{T^\prime(0)}{1!}v+\frac{T^{\prime\prime}(0)}{2!}v^2+,\dots,\frac{T^n(0)}{n!}v^n+\frac{T^{n+1}(\theta v)}{(n+1)!}v^{n+1}$, där $0<><>$

Nu råkar det vara så att $T(0)=T'(0)=0$ så den första nollskilda termen är term nummer tre.

Sen är det upp till hur du vill uppskatta felet. Eftersom jag gjort det här tidigare vet jag att nästa term är noll samt att det är en $v^3$ och en $v$ i den vilket gör den lite krångligare att felestimera, men det är inte tänkt att en "förenkling" ska göra det svårare. Det viktiga är att du förstår vad du gör och varför.

Slutligen bildar du en kvot mellan det maximala felet och approximationen. Det är denna kvot som ska vara mindre än $10^{-6}$ för hastigheter $v<>$

Jag har börjat om från början men vad händer med resttermen? Det står i uppgiften att man ska approximera T(v) med den första icke-försvinnande termen, så räcker det bara att svara med m*(v^2)/2 och strunta i resttermen?

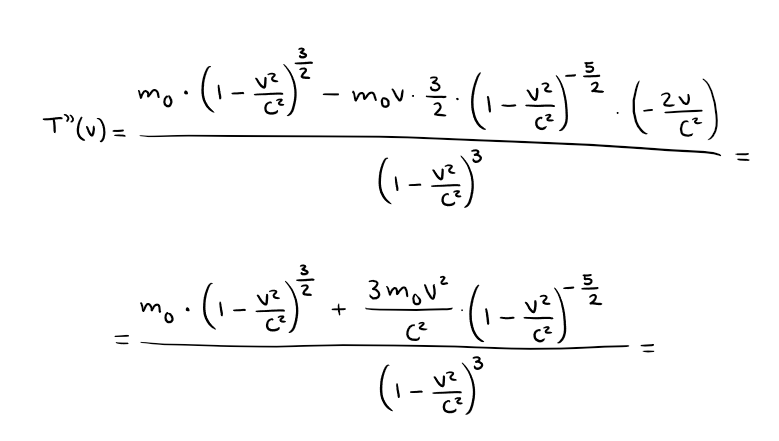
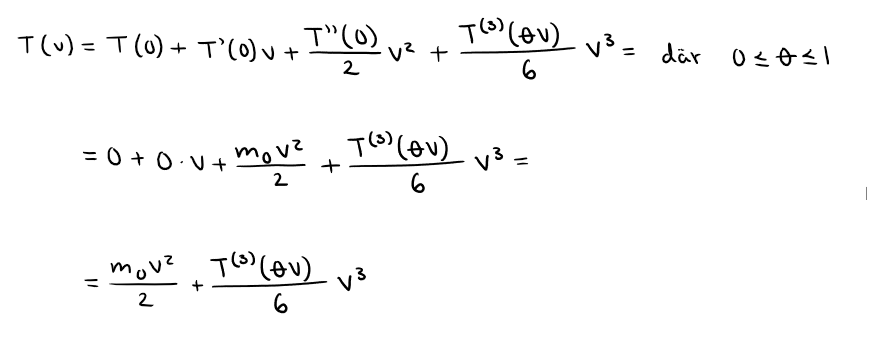
Och varför ska jag bilda en kvot i b)? Räcker det inte att approximera resttermen?

Ja, den klassiska approximationen är

$\displaystyle T\approx \frac{m_0v^2}{2}$

En formel som bör vara bekant från gymnasiefysiken (rörelseenergin enligt Newtonsk mekanik).

Orsaken till att vi söker kvoten mellan det största möjliga felet och approximation är att det står i uppgiften att man söker det relativa felet.

Tillägg: 14 dec 2022 00:55

Nu när jag tänker på saken kanske du måste gå förbi $T^3(0)v^3$-termen (den blir som sagt noll) och studera felet i $T^4$ som är nästa nollskilda term för att nå ned till $10^{-6}$