MacLaurin polynom av grad 3
Hej! Jag har kört fast på beräkningen av MacLaurin-polynomet av grad 3 till funktionen 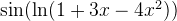 Jag har börjat med att substituera på följande vis:
Jag har börjat med att substituera på följande vis:
sin (s)
där s = ln (1+t)
och där t = 3x - 4x2.
Sedan har jag fortsatt med att utveckla ln (1+t) till .
Om jag har förstått det rätt så behöver jag endast utveckla tills jag har ett polynom av grad 3. När jag substituerar t med 3x - 4x2 får jag , där jag dessutom får en term med grad 4. Det sista steget kändes inte helt rätt och jag vet inte riktigt hur jag ska fortsätta.
Välkommen till Pluggakuten!
Man kan skriva om uttrycket som:
sin(ln(1-x) + ln(1+4x))
Tack Jan!

Svaret jag fått fram står understruket i rött, däremot är det fel. Har jag tänkt helt fel eller är det bara slarvfel?
Vad skall svaret bli?
Det vet jag tyvärr inte :(
Jag använder WebWork som funkar som ett formulär där man knappar in sitt svar och sedan får man antingen ett grönt eller rött resultat.
Testa med
sin(ln(1-x) + ln(1+4x)) = sin(ln(1-x))•cos(ln(1+4x)) + cos(ln(1-x))•sin(ln(1+4x))
Enligt WolframAlpha är du rätt nära. x3 termen är fel enligt nedanstående.

Skrev in svaret och det var rätt!! Ska försöka lösa mig fram igen med det nya uttrycket.
Uppskattar hjälpen :)


