Ma2b (gymnasienivå)

Hej och välkommen till Pluggakuten!

Jag hjälper dig med den första uppgiften så får du starta en ny tråd för den andra uppgiften.

Rita en skiss som visar trädet, käppen, solen och skuggorna. Sätt ut de mått du känner till.

Du kan sedan i din skiss försöka hitta två rätvinkliga trianglar.

Dessa trianglar är likformiga.

Kommer du vidare då?

Hej, tack! Jag vet inte hur man räknar ut skugga så det här vad det jag kunde rita.

Har du lärt dig något om likformighet?

Jag känner igen namnet men har tyvärr inte lärt mig det..

Om du har två figurer med lika stora vinklar mellan sidorna så är förhållandet mellan motsvarande sidors längd samma, se bild:

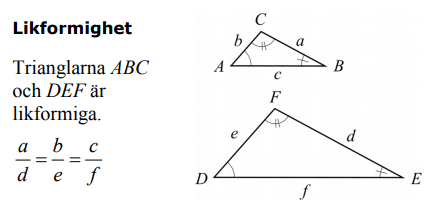
Hjälper det dig framåt?

Wazt.1995 skrev:

Hej, tack! Jag vet inte hur man räknar ut skugga så det här vad det jag kunde rita.

Bra början.

Jag har lagt till måtten, dvs käppens höjd och skuggornas längder. Trädets höjd kallar jag x.

Sorry, jag är kass när det kommer till matte men jag ska försöka, hur är vinklarna lika stora? Jag kan inte se det med blotta ögat så jag föstår inte riktigt...

Så man räknar ut skuggan genom att rita ett grafsystem?

Du får tänka att solen lyser från samma vinkel på både trädet och stolpen, då blir vinklarna i båda trianglarna lika stora. 

Sorry jag förstår inte riktigt, om solen lyser ner på läppen och trädet så att vinklarna blir lika stora, borde inte röda och blå linjen ha samma längd?

Eftersom trädet och käppen är olika höga kommer ingen av sidorna vara lika långa, men vinklarna är desamma. Trianglarna är alltså likformiga.

När trianglarna är likformiga gäller att förhållandet mellan respektive sidor i den lilla och den stora triangeln är samma. Förhållandet för skuggornas längd "träd:käpp" är 8 : 0,65. Förhållandet mellan höjden av objekten "träd:käpp" är x : 1,4, men nu vet vi inte vad x är. Vi vet dock att förhållandet 8 : 0,65 är samma som förhållandet x : 1,4. Förhållanden kan också uttryckas som bråk.

Skuggornas längd: $\frac{8}{0,65}$

Objektens höjd: $\frac{x}{1,4}$

Det viktiga är att bestämma vilket av objekten som är i täljaren respektive i nämnaren och vara konsekvent med det i alla bråkförhållanden. Du hade alltså lika gärna kunnat skriva $\frac{0,65}{8}$ och $\frac{1,4}{x}$. Men låt säga att vi valde sättet jag beskrev först.

Eftersom förhållandena är lika så är $\frac{8}{0,65}=\frac{x}{0,65}$. Kan du lösa ut x ur ekvationen?

Anledningen till att jag valde det första sättet att skriva det är att det kan vara enklare att lösa ut x om det står i täljaren från början. 

Tack för din tydliga genomgång. Jag vet inte hur man löser ut x i den ekvationen, kan man använda sig av denna graf?

Wazt.1995 skrev:

Tack för din tydliga genomgång. Jag vet inte hur man löser ut x i den ekvationen, kan man använda sig av denna graf?

Inventera bråket!

$$\begin{gathered} \frac{8}{0,65}= \frac{x}{0,14} \\ 8 \times 0,65 = 0,14 \times x \end{gathered}$$

Känner du igen detta/ är du med? Fixar du resten? Om inte, fråga!

Tack för svar, jag hänger inte riktigt med eftersom jag trodde att man skulle använda ÷ istället för x, d.v.s 8 ÷ 0,65? I.o.m att det är bråk?

Wazt.1995 skrev:

Tack för svar, jag hänger inte riktigt med eftersom jag trodde att man skulle använda ÷ istället för x, d.v.s 8 ÷ 0,65? I.o.m att det är bråk?

Jo men för att lösa ut x är det enklast att ta inversen av bråket (vet inte om metoden heter så). Ser nu att jag skrev lite fel innan. Det ska stå

$8 \times 0,14 = 0,65 \times x$

Sådan typ av bråk är enklast att lösa så (enligt mig)

För att sedan kunna lösa ut x.

Hur skulle du göra om det stod $\frac{x}{2}=1$? Förklara gärna så detaljerat som möjligt :)

Tack för svaren, ursäkta sena svaret. X $÷$ 2 = 1 = x gånger 1 = 2?Sorry kommer inte längre än så.

Wazt.1995 skrev:

Tack för svaren, ursäkta sena svaret. X $÷$ 2 = 1 = x gånger 1 = 2?Sorry kommer inte längre än så.

Precis. Alltså är x = 2

Detta kan du även se genom att sätta in "2" där det står "x". I detta fallet blir det 

$\frac{2}{2}=1$

Yes, så jag antar att syftet med frågan var hur man löser x i en ekvation?