M4) Trig. ekvationer, varför fel?
M4) Trigonometri
Var i min omskrivning blir det fel?
sin2(x)=cos2(x)
sin2(x) = 1-cos2(x)
cos2(x)=1-cos2(x)
2cos2(x)=1
cos2(x)=0.5
cos2(x)=(cos(2x)+1)/2
(cos(2x)+1)/2=0.5
cos(2x)+1=1
cos(2x)=0
Men detta stämmer inte enligt GeoGebra, som visar:
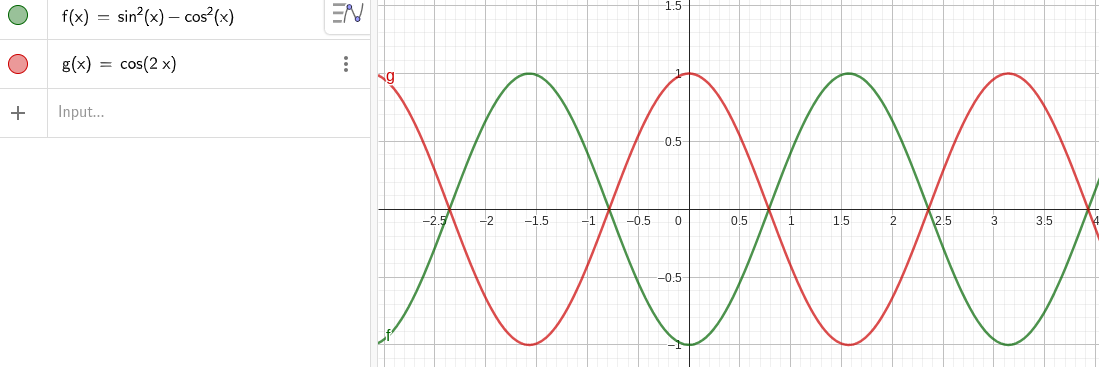
Det är tydligt att jag tappar bort ett minustecken någonstans, men jag hittar inte var.
Tack på förhand.
Vi hamnar någonstans mitt i din lösning av något. Kan du lägga upp utsprungsproblemet?
Problemet är att lösa ekvationen sin2(x)=cos2(x).
Tillägg: 16 maj 2024 13:22
(Man får inte använda några digitala hjälpmedel för att lösa uppgiften.)
Ju fler omskrivningar desto större risk för retfulla räknefel. Här ett något tydligare förslag med konjugatregeln.
sin2x=cos2x <==> sin2 x-cos2x=0 <==> (sin x+cos x)(sin x -cos x)=0 Nollproduktregeln ger två ekvationer. Ännu enklare är att ta kvadratroten ur båda leden i ursprungsekv och få samma resultat: sin x =+/- cos x. Kommer du vidare därifrån?
Tack för svaret Tomten.
Om man tar rotenur av båda led, då måste man få ett x-värde för vilket sin(x)=cos(x) och det enda är ju pi/4, och 5pi/4: stämmer det?, dvs. pi/4 + n·pi.
Mesopotamia skrev:Var i min omskrivning blir det fel?
Problemet är nog att du blandar ihop ekvationer och funktioner.
Ekvationerna sin2(x) = cos2(x) och cos(2x) = 0 har samma lösningsmängder, vilket du har visat och vilket även Geogebra visar.
Men det betyder inte att funktionerna f(x) = sin2(x)-cos2(x) och g(x) = cos(2x) är identiska.
Jaha, det har jag aldrig stött på.
Kan du snälla förklara mer?
Mesopotamia skrev:Jaha, det har jag aldrig stött på.
Kan du snälla förklara mer?
Säg att vi har en funktion h(x) och att vi med den sätter upp en ekvation h(x) = 0.
Dvs vi letar efter nollställen till funktionen.
om vi nu subtraherar h(x) från båda sidor av ekvationen (alternativt multiplicerar hela ekvationen med -1) så får vi 0 = -h(x).
Denna ekvation har självfallet samma lösningsmängd som den ursprungliga ekvationen.
Dvs h(x) = 0 har samma lösningar som -h(x) = 0.
Men det betyder ju inte att h(x) = -h(x).
Tack för svar Yngve. Då är jag med på vad du menar.
Men har jag svarat rätt?, se inlägg #5?
Mesopotamia skrev:Tack för svar Yngve. Då är jag med på vad du menar.
Men har jag svarat rätt?, se inlägg #5?
Nej, du glömmer ± och tappar därmed bort hälften av lösningarna.
Om du följer tipset från Tomten i svar #4 så kommer du fram till de två ekvationerna
- sin(x)=cos(x), med lösningar x=π4+nπ
- sin(x)=-cos(x), med lösningar x=3π4+nπ
Sammantaget ger det lösningsmängden x=π4+nπ2
Då förstår jag.
Tack Yngve för hjälpen.


