M4) Komplexa tal, varför fel?
M4) Komplexa tal
43
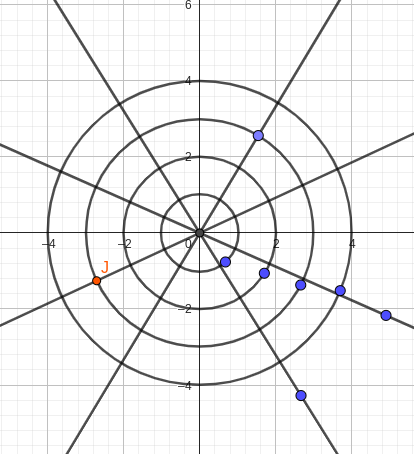
I det komplexa talplanet ovan finns 4 cirklar med mittpunkt i origo.
4 linjer delar varje kvadrant i tre lika stora cirkelsektorer.
Vilken av skärningspunkterna mellan linjerna och cirklarna uppfyller samtliga villkor nedan?
- z och z* finns bland skärningspunkterna
- arg z > arg z* räknat motsols från positiva realaxeln
- 2z eller z/2 finns inte bland skärningspunkterna
- 0 > Re z3
Jag har kommit fram till att J är den punkten, men det är fel enligt facit.
Kan någon förklara varför?
Om vi betraktar J som z, finns z*.
Arg z är större än arg z*.
2z eller z/2 finns inte bland skärningspunkterna.
Re z3 = (-3)3 = -27 vilket ju är mindre än noll.
Tillägg: Nu när jag funderat mer inser jag att det sista kravet är felaktigt. Jag borde räkna ut z3 och sedan kontrollera realdelen av det talet. Visst?
Varför stämmer inte detta?
Tack på förhand.
(Ignorera de lila punkterna i bilden; de har ingen betydelse.)
Har du någon kvarvarande fråga kring detta och hur lyder i så fall den?
Tips:
Jag skulle ta villkoren i följande ordning.
- Villkor 3 utesluter flera av cirklarna
- Villkor 4 utesluter en del av linjerna
- Villkor 2 utesluter ytterligare linje(r)
- Villkor 1 ska utesluta alla utom en av de kvarvarande skärningspunkterna
Hej Yngve, tack för att du återkopplar och tack Jan Ragnar för din förklaring.
Jag ska försöka mig på en lösning igen och återkommer om jag fastnar.




