Lutande plan och kraftekvationen
Hej! Uppgiften:
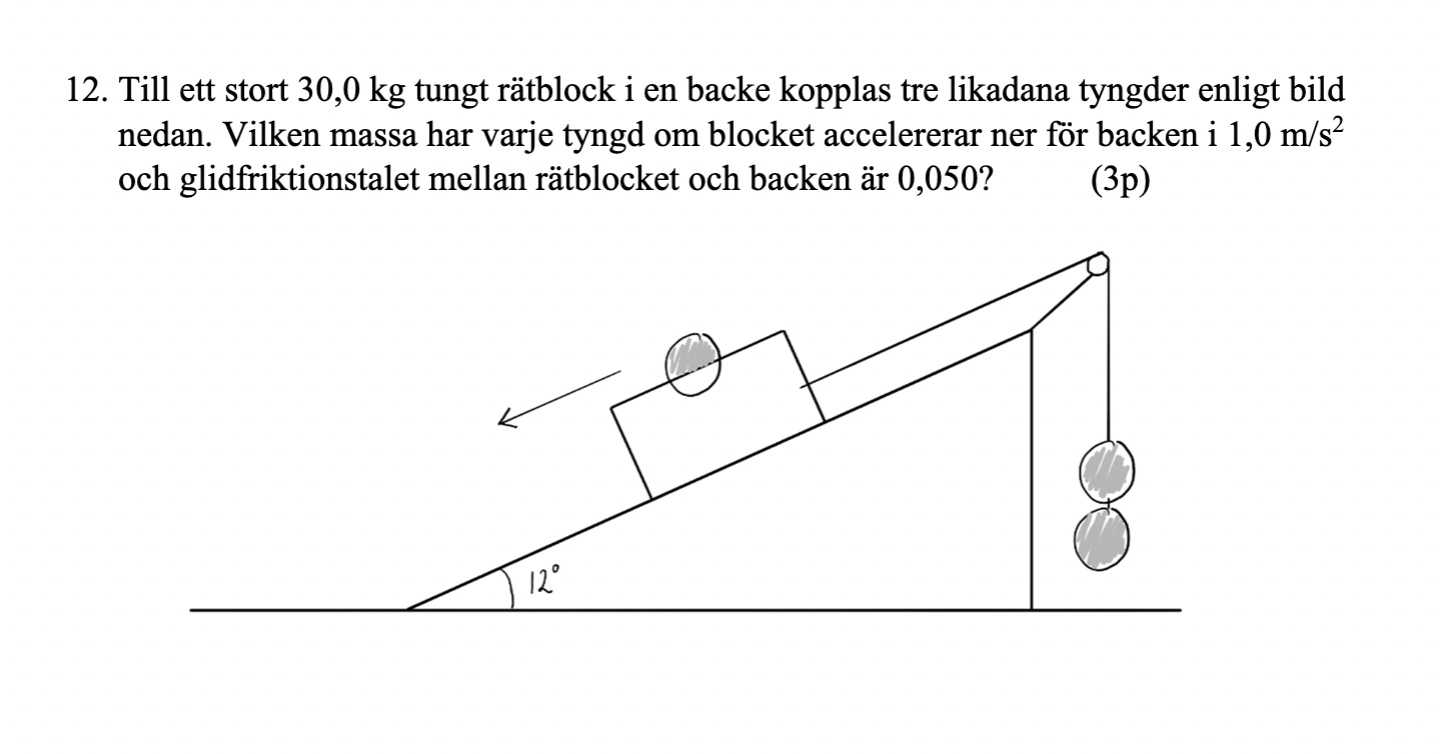
Min lösning:

Hoppas den inte är svår att följa i och med många insättningar av uttryck. Svaret ska bli 0,80 kg. Vad gör jag för fel? Kan man lösa den på ett effektivare sätt? Tack!
den totala massan som accelererar är 30+3m där en liten vikt är m.
Du har räknat med 30+m enbart, eftersom du gjorde fel i friläggningen av de vertikala kulorna
Frilägg tyngden på planet
(30+m)a = Ftyngdkraftskomposant(30+m) - Ffriktion - S
Ftyngdkraftskomposant är (30+m)g*sin(12)
F friktion är (30+m)g*0,05*cos(12)
S får man genom friläggning av de vertikala tyngderna (positiv riktning uppåt analogt med tyngden på planets positiva riktning)
S-2mg = 2ma här dök de 2 ma upp som jag saknade tidigare.
Sätt ihop allt så får du
(30+m)a = (30+m)g*sin(12) - (30+m)g*0,05*cos(12) - 2ma-2mg
Du gjorde exakt samma fel som Yngve i denna tråd:
Du skriver att vilket är fel då tyngderna som hänger vertikalt accelererar. Enda sättet att lösa en uppgift med många nödvändiga substitutioner "effektivare" är att hoppa över vissa algebraiska steg. Du introducerade dock många icke nödvändiga substitutioner med många märkliga och onödiga uttryck så som detta till exempel:
Detta är egentligen:
Detta kunde du lämnat som det var men du ville bestämt skriva om det i termer av och av någon oklar anledning.
Alltså, ett helt överflödigt arbete med substituering.



