Lösning på gammal uppgift
Hej. Håller på med lite äldre uppgifter men förstår inte riktigt hur "facit" har gått till väga.
Uppgift:
Bestäm samtliga lösningar till ekvationen 4sin(x)=sin(2x). (Svara exakt i grader)
Dubbla vinkeln ger 2sinvcosv i HL.
I sista steget så gör facit något som jag inte förstår hur dem gör.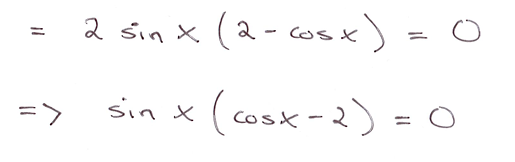 Att man delar med två för att få bort 2an framför sinx är jag helt med på. Men var tar minustecknet vägen?
Att man delar med två för att få bort 2an framför sinx är jag helt med på. Men var tar minustecknet vägen?
-cosx är ju inte cosx, däremot är (Cos(-v)=cos(v)). Men det finns ju inte här?
Lite slarvigt att inte visa stegen på väg dit men så här har de nog tänkt:
Jag förstår dock inte varför de gör dessa steg, för det behövs inte för lösningen!
SvanteR skrev:Lite slarvigt att inte visa stegen på väg dit men så här har de nog tänkt:
Jag förstår dock inte varför de gör dessa steg, för det behövs inte för lösningen!
Ok, har problem att lösa uppgiften. Så att det inte behövs för lösningen är jag inte helt med på :P
Men okej, man gångrar alltså med (-1) så man får: (Jag tar det i alla steg för jag vill förstå hur man går till väga i varje steg)
!
Antar det är så? :)
Efter att ha använt formeln för dubbla vinkeln får man 2 sin(x)(2-xos(x)) = 0.
Om en produkt av tre termer skall bli 0, måste (minst) en av termerna vara 0.
2 kan aldrig ha värdet 0.
När är sin(x) = 0?
När är 2-cos(x) = 0?
Smaragdalena skrev:Efter att ha använt formeln för dubbla vinkeln får man 2 sin(x)(2-xos(x)) = 0.
Om en produkt av tre termer skall bli 0, måste (minst) en av termerna vara 0.
2 kan aldrig ha värdet 0.
När är sin(x) = 0?
När är 2-cos(x) = 0?
Resten av lösningen borde bli:
Lösning 1:
Lösning 2:


