Lösa tredjegradsekvation vid diagonalisering
Hej!
Jag pluggar inför tenta i linjär algebra och har nu flera gånger stött på uppgifter där man, om möjligt, ska diagonalisera en matris A. Se t.ex. uppgiften här nedan som jag försöker lösa. Dessa slutar ofta i en tredjegradsekvation som jag inte vet alls hur jag ska lösa (och dessutom en lång förenkling innan jag ens kommer fram till hur många jag har av varje variabel...)
Min fråga är, ska det vara så här tidskrävande? Eller finns det en enklare metod? Och som i exemplet här blir jag osäker hur jag ens ska lösa ekvationen. Det var några år sen jag gick på gymnasiet så kommer inte riktigt ihåg hur man löste tredjegradsekvationer... :)
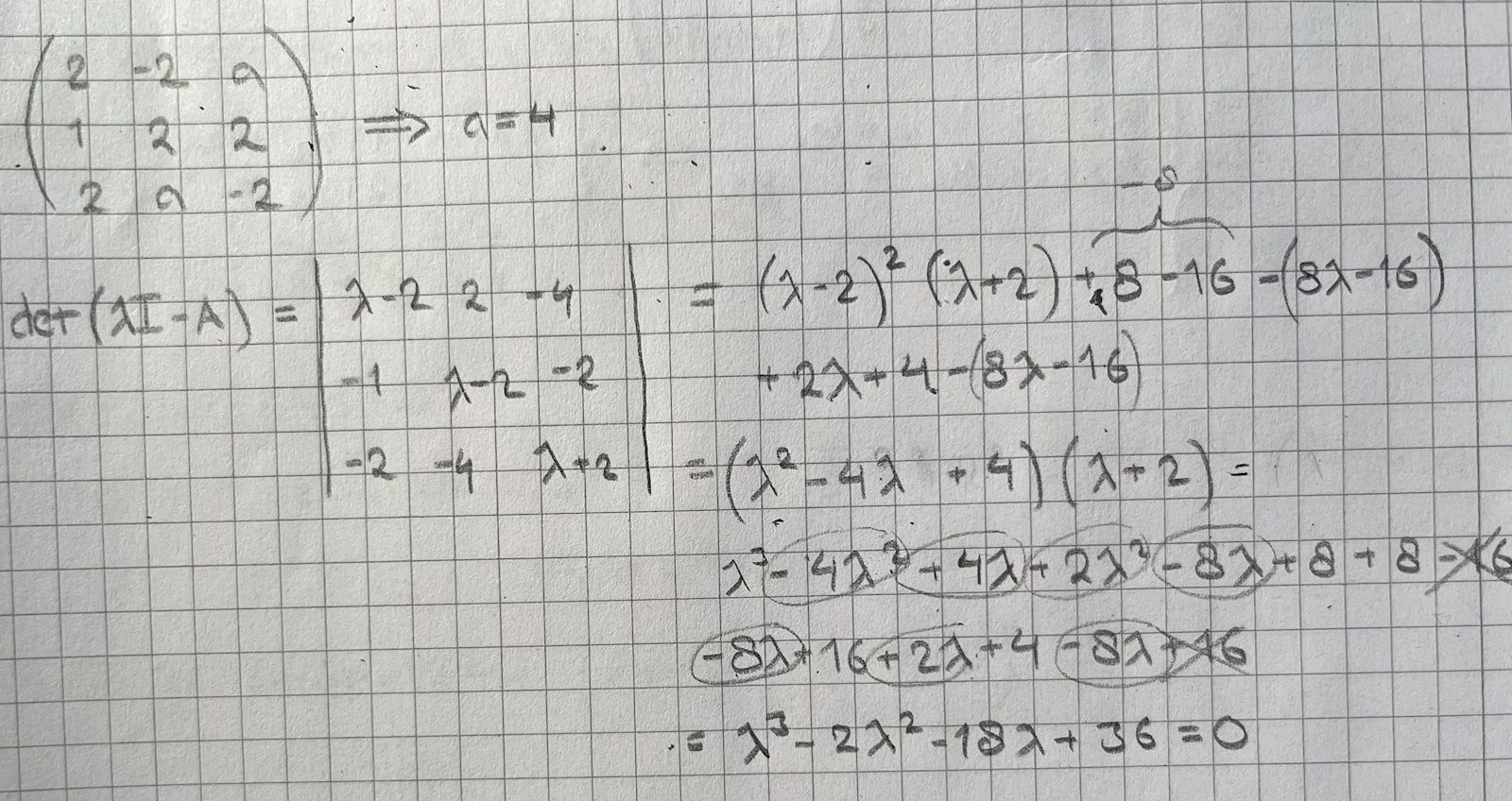
Hej,
När det gäller tredjegradsekvationer är de inte helt enkla att lösa. Det finns visserligen en formel för det men inte som är värd att skriva ner med penna och papper.
Den vanligaste lösningsmetoden är att man "gissar" till sig första roten. Detta funkar inte alltid men i sådana här uppgifter (där poängen inte är att lära sig lösa tredjegradsekvationer) bör det gå. Exempelvis kommer vara en lösningen för denna ekvation. Därefter vill du bryta ut en term och lösa den återstående andragradsekvationen.
Dessutom har du räknat fel på ditt uttryck 
Du behöver inte räkna ihop parenteserna då du härifrån ser att om så blir resultatet = 0
Och i första parentesen syns det att det är en dubbelrot där ,
Mattemats skrev:Dessutom har du räknat fel på ditt uttryck
Du behöver inte räkna ihop parenteserna då du härifrån ser att om så blir resultatet = 0
Och i första parentesen syns det att det är en dubbelrot där ,
Tack för uppmärksammandet! Men, jag har varit lite slarvig med "lika-med"-tecknet. För min ursprungliga ekvation:
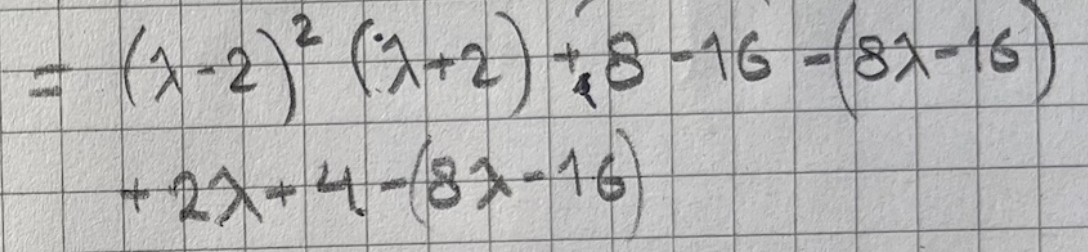
Är ju inte enbart lika med

som det ser ut i min uppgift. Utan det som du visar i bilden du infogat är ju enbart första delen i ekvationen som jag utvecklat. Och då tänker jag att det inte räcker med att se att t.ex. lambda = -2 ger att en parantes = 0, för eftersom det är en massa fler additioner och subtraktioner i uttrycket så blir ju inte allt lika med 0 ändå. Och då är inte V.L. = H.L. Eller tänker jag fel?
Calle_K skrev:Hej,
När det gäller tredjegradsekvationer är de inte helt enkla att lösa. Det finns visserligen en formel för det men inte som är värd att skriva ner med penna och papper.
Den vanligaste lösningsmetoden är att man "gissar" till sig första roten. Detta funkar inte alltid men i sådana här uppgifter (där poängen inte är att lära sig lösa tredjegradsekvationer) bör det gå. Exempelvis kommer vara en lösningen för denna ekvation. Därefter vill du bryta ut en term och lösa den återstående andragradsekvationen.
Tack! Jag förstår, tråkigt att behöva gissa men antar det är vad som kanske är smidigast. Men hur bryter man ut en term (lambda - 2)?
Det kan inte vara bra att slarva med likhetstecken.
I mer realistiska fall får man nog en gräslig tredjegradsekvation som man bara kan lösa med numeriska metoder. I sådana här uppgifter är det oftast meningen att man ska hitta någon enkel rot, 2 i det här fallet.
För att hitta de övriga får man polynomdividera determinantuttrycket med -2.
Jag vet inte vilken metod du använde för determinanten. När jag provar den jag kan så ser jag rätt snabbt (om än inte omedelbart) att 2 är ett nollställe. Det kanske är så uppgiftsskrivaren har tänkt.
Laguna skrev:Det kan inte vara bra att slarva med likhetstecken.
I mer realistiska fall får man nog en gräslig tredjegradsekvation som man bara kan lösa med numeriska metoder. I sådana här uppgifter är det oftast meningen att man ska hitta någon enkel rot, 2 i det här fallet.
För att hitta de övriga får man polynomdividera determinantuttrycket med -2.
Jag vet inte vilken metod du använde för determinanten. När jag provar den jag kan så ser jag rätt snabbt (om än inte omedelbart) att 2 är ett nollställe. Det kanske är så uppgiftsskrivaren har tänkt.
Nej det har du rätt i. Jag hade inte planerat att lägga upp en bild på min lösning här på Pluggakuten, därav att jag inte tänkte på att rätta till mina egna slarviga anteckningar.
Jag antar att det inte finns fler metoder att räkna ut determinanten än det jag gjort i min bild. Se bilden här nedan, som visar ett annat exempel men precis samma metod som jag använt mig av (och alltid använder).
Med den metoden kan, åtminstone inte jag, direkt se att 2 skulle vara ett nollställe i min uppgift. Visst att jag får en parantes (lambda - 2) som skulle bli 0 om jag satte in att lambda = 2, men bara för att den parentesen är 0 så gör inte det att hela vänsterledet blir lika med 0. Därmed kan jag inte heller dra slutsatsen att lambda = 2. Rätta mig om jag har fel. :)
Du har sex produkter där, och alla utom två har faktorn lambda-2. Man kan råka observera att summan av de två återstående också är en multipel av lambda-2, men det kanske inte är så lätt ändå.




