Lösa svåra exponentiella ekvationer med geogebra

Jumsan_j skrev:

Hej! Jag lyckas inte få fram alla svar för denna fråga:

 

Lös ekvationen med digitalt hjälpmedel.

$2\times 1,{05}^t=t^2$

Jag la in högerledet och vänsterledet som två separata grafer i geogebra, och hittade skärningspunkten mellan dem, vilket var t=ca 204

 

Detta stämde, men facit har två svar till. Jag vet inte hur jag ska få fram dessa. Det fanns inget "lös" alternativ i geogebra som det brukar. Borde det inte finnas fler skärningspunkter? Någon som kan hjälpa?

 

Tack i förhand!

Nära origo är t^2 "kraftigast" och 1.05^t "svag"

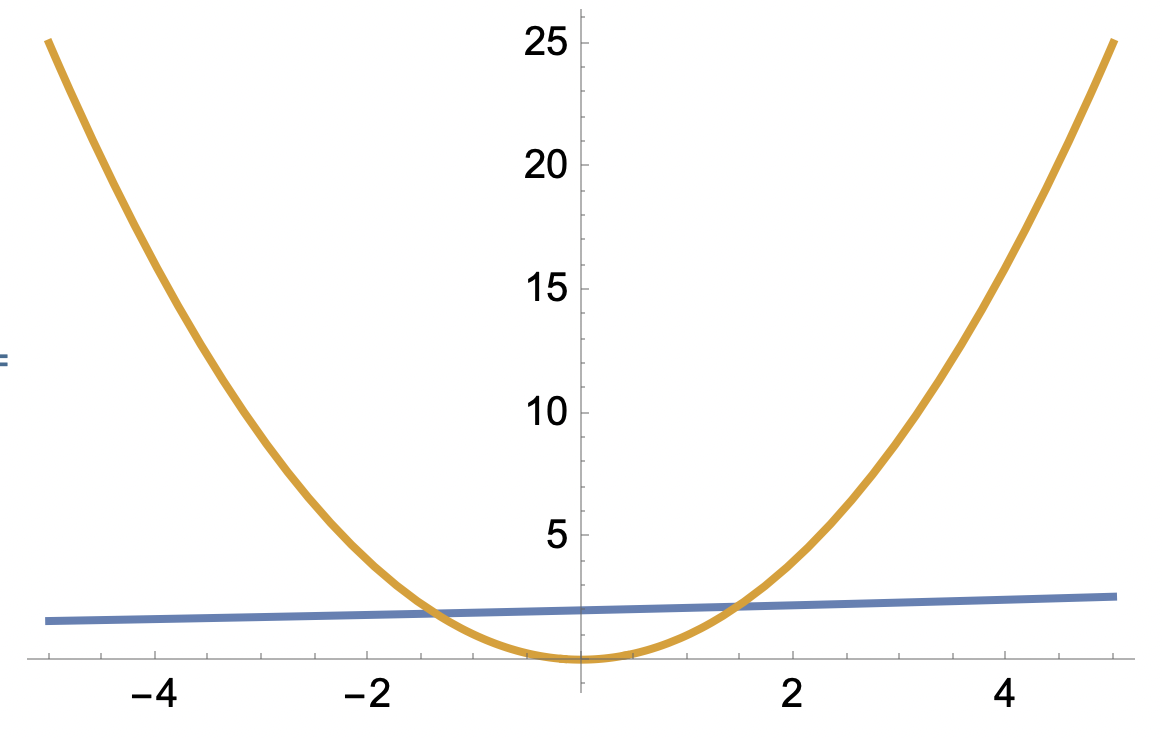
Men, 1.05^t kommer alltid att "vinna över" ett polynom i längden;

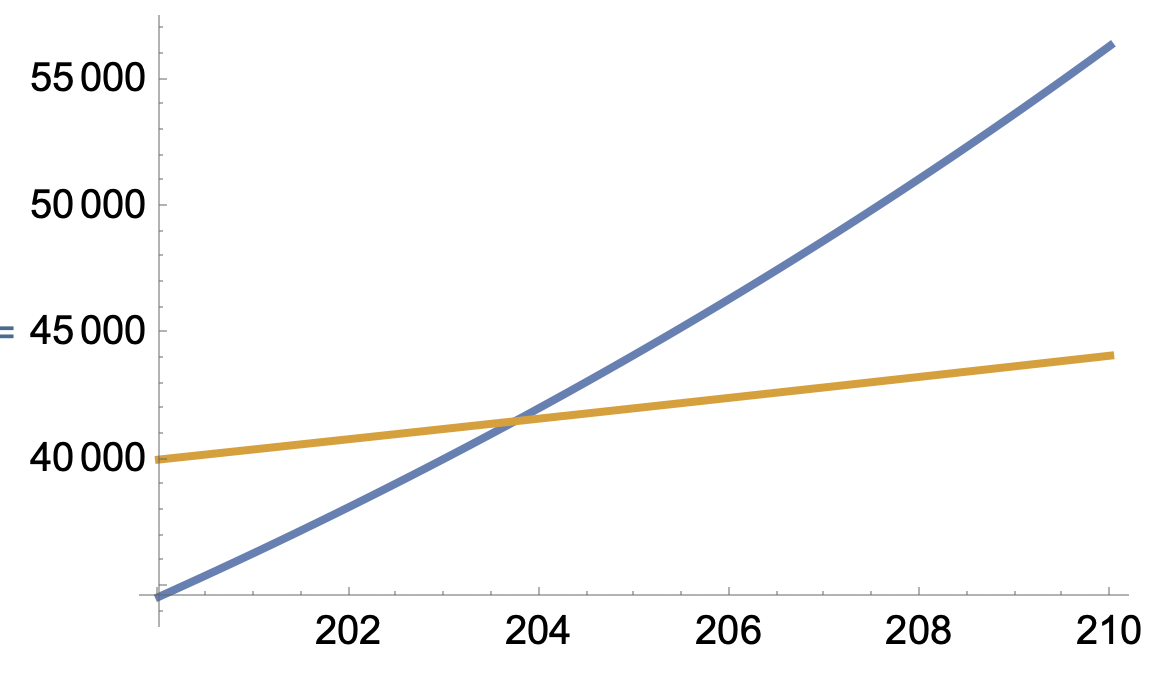
ok tack! Men hur kommer det sig att geogebra inte visar alla skärningspunkter?

Hur ser det ut med geogebra?

Jag tror det beror på att spannet är stort;

både i t- och "y"-led.

Har Geogebra log-log-plot så kan det bli tydligare på den positiva sidan, men man får se upp med den negativa;

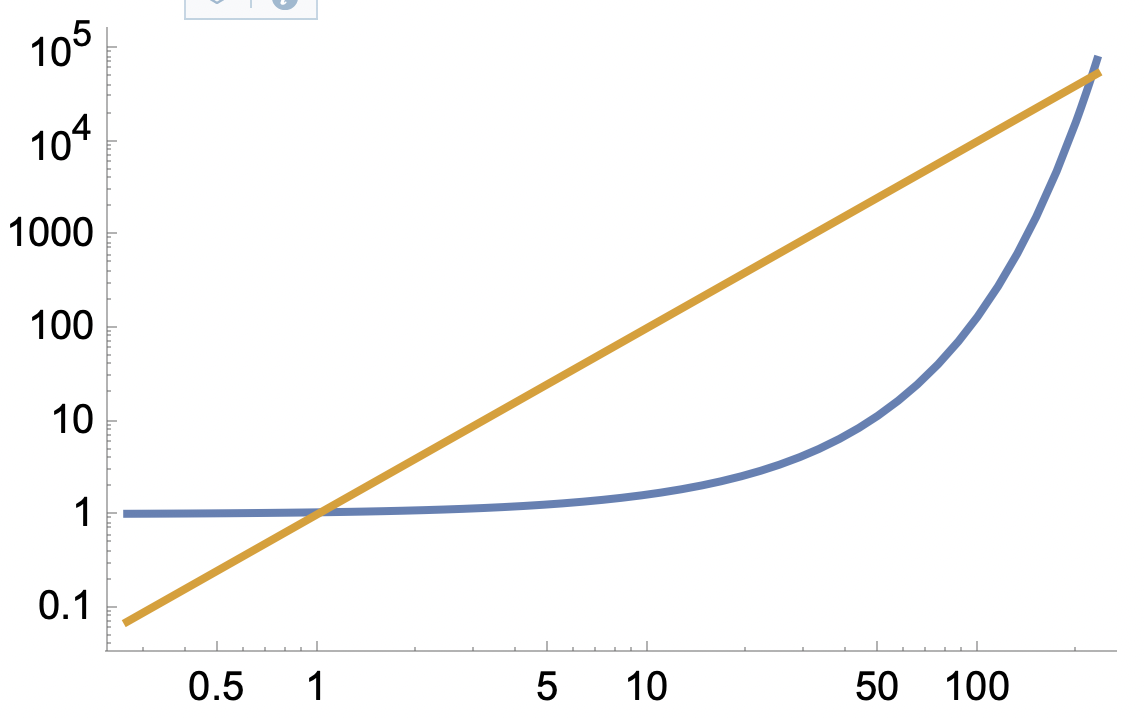
här får man dock se upp då t-axeln är en log-skala. Log-plot kanske då är bättre;

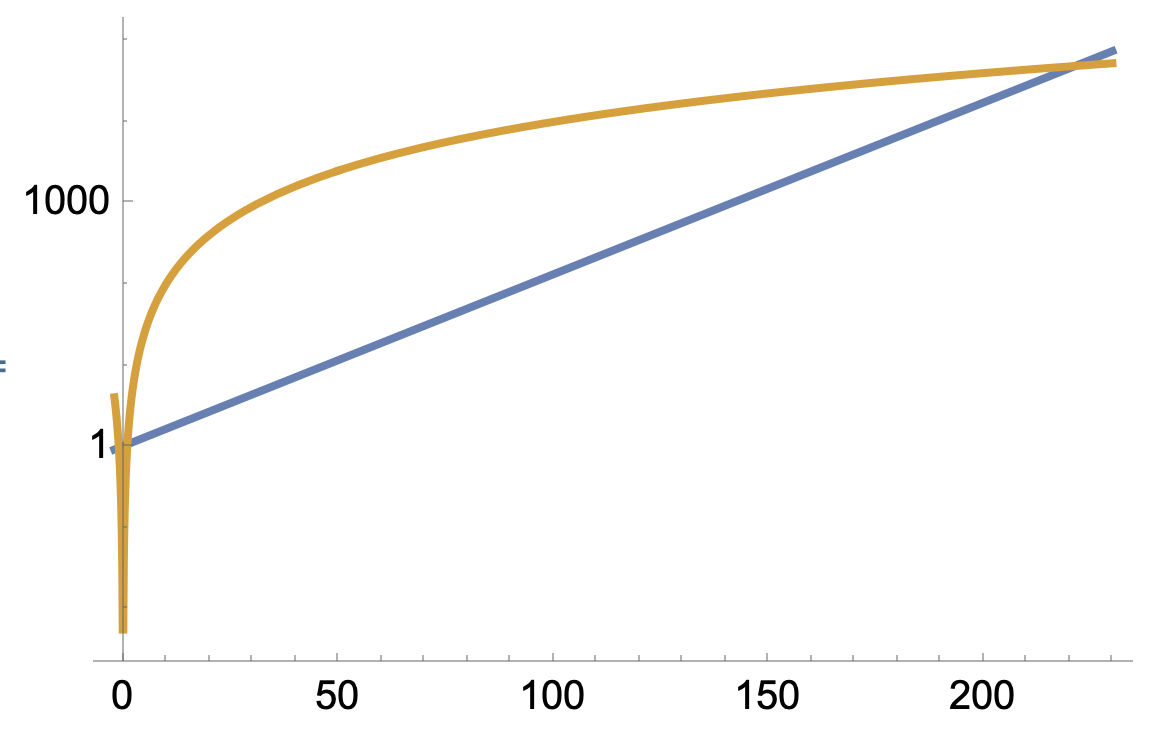
där endast "y"-axeln är transformerad.

Även här blir det svårt att se att det är 2 skärningar för små t-värden, men lite tydligare än första grafen.