Lösa optimeringsuppgift på funktionsyta

Ytans ekvation kan du skriva som g(x,y,z) = 2 (eller = 0, smaksak).

I vilka punkter är gradienterna av f(x,y,z) och g(x,y,z) parallella?

Dr. G skrev:

Ytans ekvation kan du skriva som g(x,y,z) = 2 (eller = 0, smaksak).

I vilka punkter är gradienterna av f(x,y,z) och g(x,y,z) parallella?

Tack för ditt svar!

Varför behöver man undersöka när gradienterna av $f(x, y, z)$ och $g(x, y, z)$ är parallella?

Men här är hur jag tänker:

Först definierar jag ytans ekvation som $g(x, y, z) = x^2 + y^2 + 2z^2 - 2 = 0$.

Sedan beräknar jag gradienterna:

$\nabla f = (2x, 4y, 2z)$

$\nabla g = (2x, 2y, 4z)$

För att gradienterna ska vara parallella måste det finnas en konstant $\lambda$ så att $\nabla f = \lambda \nabla g$. Det ger oss systemet:

$2x = \lambda 2x$

$4y = \lambda 2y$

$2z = \lambda 4z$

Har jag förstått det rätt? Hur går jag vidare härifrån?

Hint: Den första ekvationen säger lambda = 1 eller x = 0.

PATENTERAMERA skrev:

Hint: Den första ekvationen säger lambda = 1 eller x = 0.

Så om vi tar hänsyn till den första ekvationen $2x = \lambda 2x$, så får vi att $\lambda = 1$ eller $x = 0$. 

Om $\lambda = 1$, så ger det oss ekvationssystemet:

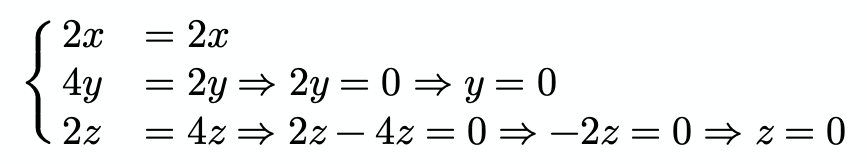
Vad gör man härifrån?

Jag hade gärna också viljat förstå varför detta steg behövs:

Varför behöver man undersöka nör gradienterna av $f ( x , y , z )$ och $g ( x , y , z )$ är parallella?

För lamda = 1 så får vi att y = z = 0. Värdet på x får vi från villkoret att vi befinner oss på ytan x² + y² + 2z² = 2. Dvs x² = 2.

Sedan får man behandla fallet x = 0.

Den andra ekvationen ger då att lambda = 2 eller y = 0.

Osv.

Att formulera med gradienter är bara ett alternativt sätt att formulera metoden med Lagrangemultiplikatorer.