7
svar
106
visningar
Lösa olikheter
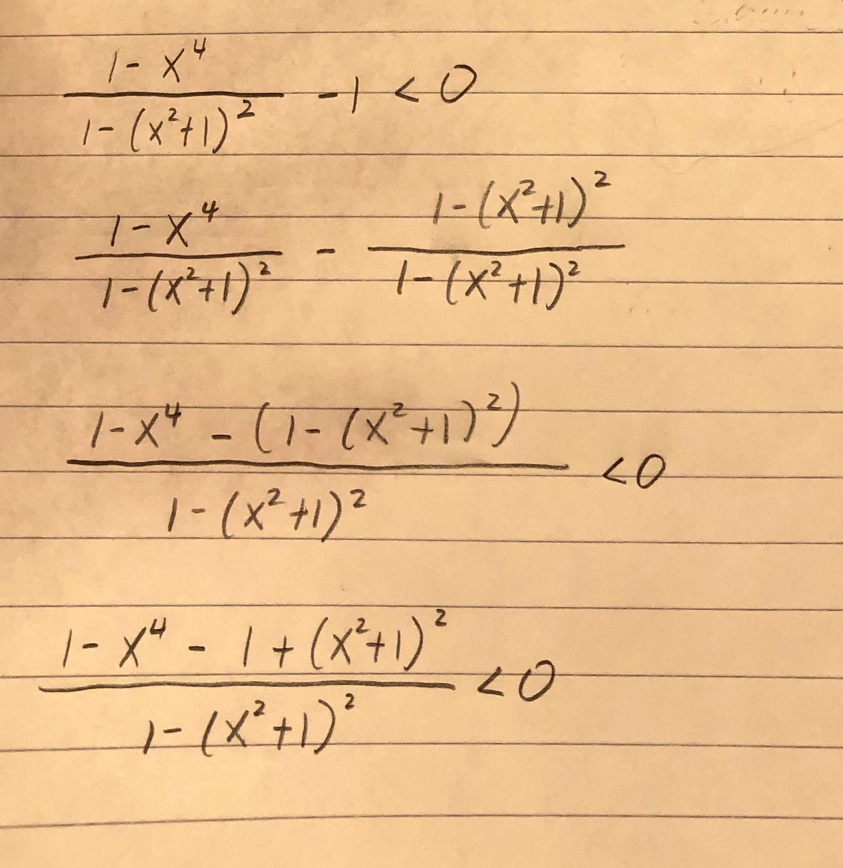
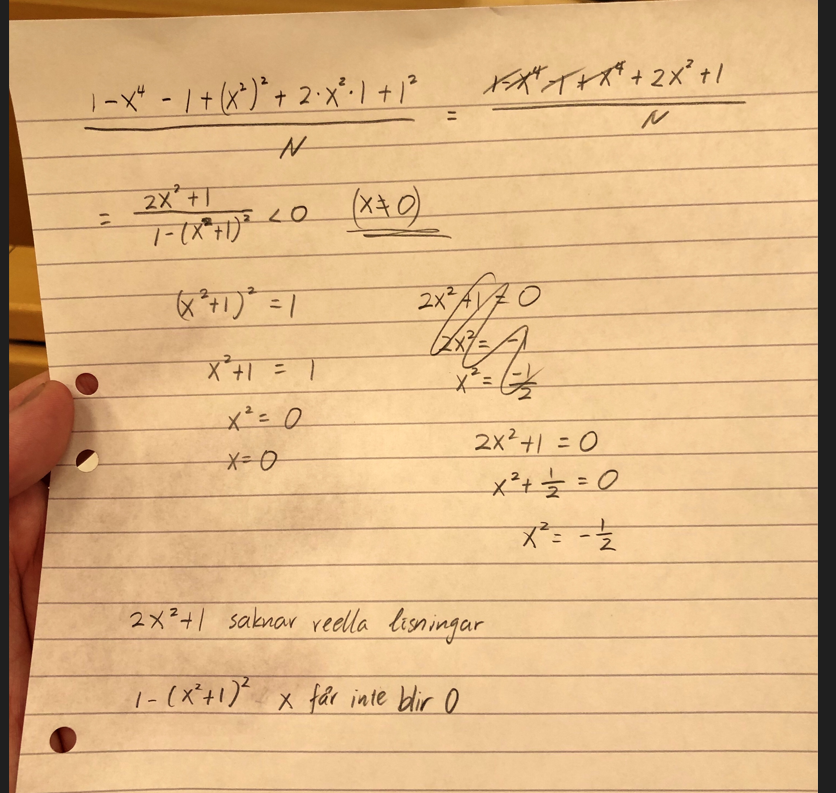
Jag vet inte hur ja ska göra min teckentabell för att det täljare har ingen reella lösning.
Jag har inte kollat dina uträkningar, men om de är rätt:
- Täljaren är alltid positiv.
- Vad måste då nämnaren vara för att kvoten ska vara negativ?
Om täljare är alltid positiv, då måste nämnaren vara alltid negativ för att kvoten ska vara negativ.
Nämnaren måste alltid vara strikt negativ.
OK, och din slutsats blir ...?
Om du menar att (x2+1)2 alltid är större än 1 så stämmer ditt resonemang.
Juste det borde jag säga. Har missat det, tack för påminnelsen.



