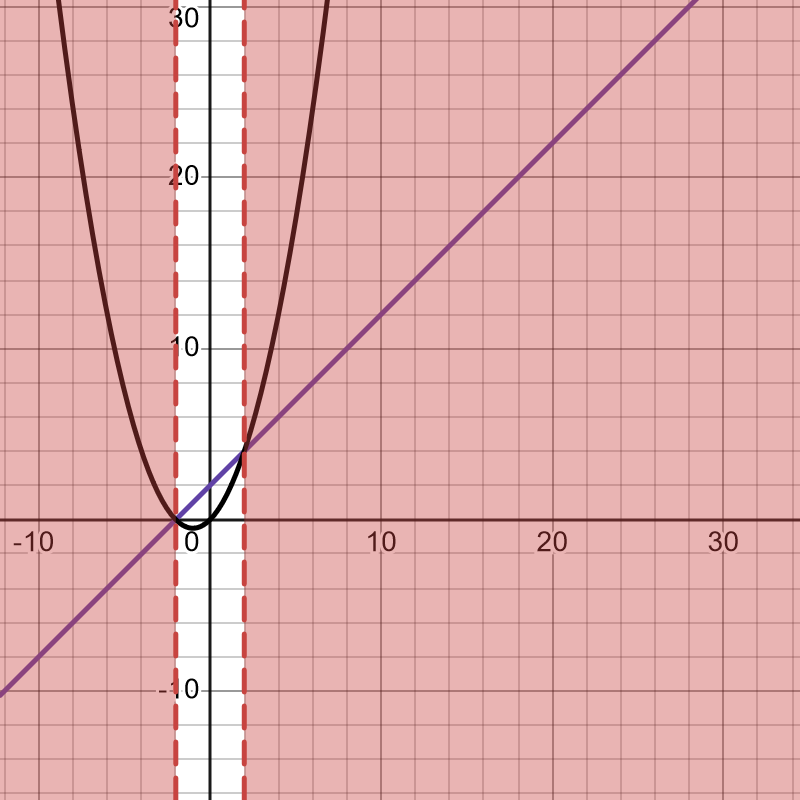
Lösa olikheten grafiskt?? jag förstår vad de menar i b men inte hur man skriver upp det

Man menar så här:
För vilka x-värden gäller olikheten?
dvs
För vilka x-värden ligger parabeln ovanför linjen?
Arktos skrev:Man menar så här:
För vilka x-värden gäller olikheten?
dvs
För vilka x-värden ligger parabeln ovanför linjen?
Är det då -2 och 2? eller ska man svara. Och varför ska man inte skriva någonting om y värdena eller de spelar ingen roll?
Det är y-värdena vi jämför.
När parabeln ligger ovanför linjen,
är det y-värdet för parabeln som ligger ovanför y-värdet för linjen
För x=-2 och x=2 skär de varandra.
Där ligger ingen ovanför den andra.
Arktos skrev:
Det är y-värdena vi jämför.
När parabeln ligger ovanför linjen,
är det y-värdet för parabeln som ligger ovanför y-värdet för linjen
För x=-2 och x=2 skär de varandra.
Där ligger ingen ovanför den andra.
ja, förstår att det är området ovanför den linjen men jag förstår inte hur man skriver det.
är det så 2<x eller hur gör man
Du ser det ju i figuren.
Man ligga till höger om den övre skärningspunkten
eller till vänster om den undre skärningspunkten.
Det är en geometrisk beskrivning av lösningen till olikheten.
Hur uttrycker man samma sak algebraiskt?
Arktos skrev:Du ser det ju i figuren.
Man ligga till höger om den övre skärningspunkten
eller till vänster om den undre skärningspunkten.
Det är en geometrisk beskrivning av lösningen till olikheten.Hur uttrycker man samma sak algebraiskt?
ja det är det jag inte fattar
I all enkelhet [ x < -2 eller x > 2 ] eller kanske { x | x < -2 eller x > 2 }
Hur gör man i kursboken?
Arktos skrev:I all enkelhet [ x < -2 eller x > 2 ] eller kanske { x | x < -2 eller x > 2 }
Hur gör man i kursboken?
okej tack!!!
detta va nämligen bara ett papper som vi fått av vår lärare så det fanns inget facit… därför blev de lite svårt o veta hur jag skulle uttrycka mig
De aktuella intervallen är de som är rödmarkerade i bilden. För det vänstra - vilka x-värden finns det där? För det högra - vilka x-värden finns det där?