Lösa likheten
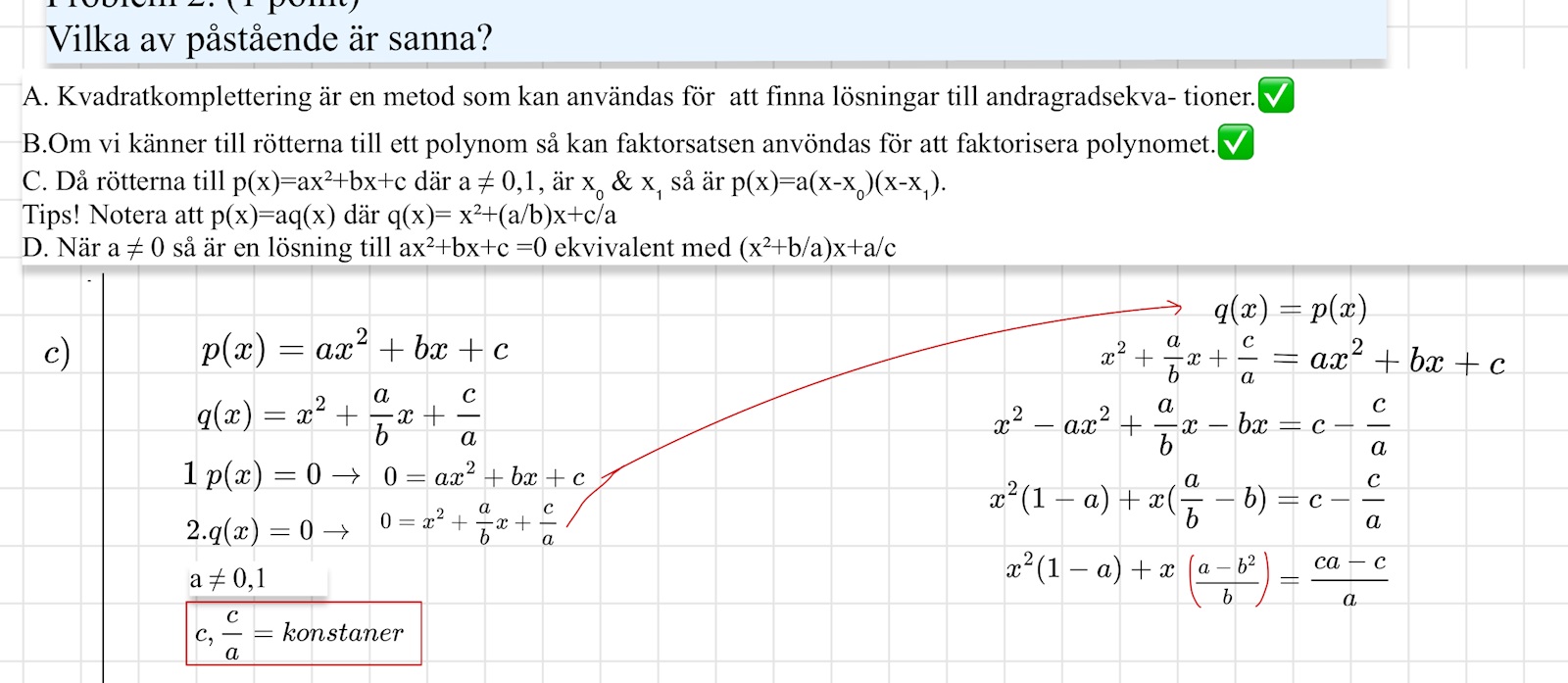
Hej jag undrar hur man kan tänk på c & d. C tänkte jag att eftersom både p(x) & q(x)= 0 försökte jag sätta de lika med varandra men vet inte hur detta hjälpte. Sen tänkte jag på ekvaktions system men har ju 3 variablar & två ekvaktioner:(
Tips: Tipset i C har ett tryckfel det ska vara b/a inte a/b
I D har uttrycken inte samma grad, sen vet inte jag hur en lösning till en ekvation kan vara ekvivalnet med ett polynom??
Jag tycker detta borde vara lätt, men finns det en quick fix så har jag missat den.
Jag kallar polynomen pA(x) respektive pB(x)
C). Koefficienten för x-termen är rötternas summa med omvänt tecken, konstanttermen är rötternas produkt.
pB(x) = a[x2 – (x1+x2)x + x1x2]
pA(x) = a[(x2+(b/a)x+c/a ] med nollställen [–b ± sqr(b2 –4ac)]/(2a)
Bildar vi summan av dessa nollställen får vi –b/a
Bildar vi produkten får vi c/a
Sätt in i ekv för pB : a[x2 + (b/a)x + c/a] = ax2+bx+c
Så pA = pB:
D) Tryckfel även här. a/c ska vara c/a. Dessutom är parentesen felskriven, om uppgiften ska ha någon mening borde det stå
… så har ax2+bx+c = 0 samma lösningsmängd som x2+(b/a)x + c/a = 0.
Lösningsmängderna är som matsC påpekar, inte ekvivalenta, de är lika.
Skilj på <=> och =.
Hej för c får jag det till
q(x)= x²+(b/a)x+c/a
p(x)=ax²+bx+c
q(x)=0
p(x)=0
Ekvation ekvivalenta ger..
p(x)=q(x)
ax²+bx+c=x²+(b/a)x+c/a
ax²+bx +c - c/a = x²+(b/a)x
ax²- x² + bx +c - c/a = (b/a)x
ax²- x² + bx -(b/a)x +c - c/a =0
Faktosering term vis
ax²- x²= x²•(a-1)
bx -(b/a)x= x•(b-b/a)
c/a-c= c•(1/a-1)
Faktorseradform
x²•(a-1)+x•(b-b/a)+c•(1/a-1)=0
men vet ej hur jag kommer vidare nu:(
Så här att de rätta påståenderna

Fast D är sant så förstår inte riktigt:(
Det som står under D i ditt första inlägg är ju något annat.
Ja jag upptäckte det:) Det var jag som var klantid när jag skrev in:(
Hej,
Ursäkta att jag flikar in i tråden, men av nyfikenhet undrar jag: vilken utbildning på universitetet ingår detta i?
Hej! Föreberedande matte kurs på stockholmsuniversitet


