Lösa en gränsvärdesuppgift med polära koordinater
Jag försöker lösa en gränsvärdesuppgift och skulle behöva lite hjälp. Uppgiften lyder:Jag har försökt att använda polära koordinater för att lösa detta, men jag är osäker på om jag har gjort rätt. Här är vad jag har gjort hittills:
Jag omvandlade och till polära koordinater:
Jag ersatte och i uttrycket:
Jag förenklade uttrycket genom att faktorisera ut i nämnaren:
Jag tog gränsvärdet när :
Jag fick resultatet att gränsvärdet är 0, men jag är inte helt säker på om jag har gjort alla steg rätt. Skulle någon kunna kontrollera detta och ge mig feedback? Finns det något jag har missat eller gjort fel?
Någon påpekade följande:
"Vad händer då eller ? När , vad händer här?Obestämt. Du behöver ta hänsyn till när är noll. Om det är obestämt, försök att bestämma det. Allt jag säger är att överväga två fall för gränsvärdet. Ett där är noll, och ett där det inte är. Och visa att du får samma gräns i båda fallen."
Men varför detta ö.h.t. behövs göras, är inte klart för mig.
Tack på förhand!
Som vi diskuterade i din tidigare tråd måste gränsvärdet existera för alla möjliga vägar vi rör oss mot punkten vi vill undersöka. I det fallet punkten är origo låter vi r->0 och alla (oändligt många) vägar bestäms av värdet på theta inom intervallet [0,2p).
För alla theta!=pi/2 och theta!=3pi/2, gäller att gränsvärdet är 0 precis som du hittat.
För theta=pi/2 och theta=3pi/2 får vi specialfall som måste hanteras för sig. Sätt helt enkelt in detta värde på theta i kvoten och undersök nu gränsvärdet då r->0.
Calle_K skrev:För theta=pi/2 och theta=3pi/2 får vi specialfall som måste hanteras för sig. Sätt helt enkelt in detta värde på theta i kvoten och undersök nu gränsvärdet då r->0.
Vad är det som behöver hanteras, egentligen? Om vi inte hittar gränsvärden som är 0, då får vi att gränsvärdet inte existerar helt enkelt, eftersom vi har funnit två fall där gränsvärdet inte blev 0 (nämligen π/2, 3π/2).
Vi får en obestämd form, 0/0 (därav en gränsvärde som inte existerar), så vad är det vi hanterar?
Gå tillbaka till ursprungsuttrycket och se vad det blir.
0<=x2y2/(x2+y4)<=x2y2/(x2+0)=y2–>0 när (x,y)—>(0,0)
Tomten skrev:0<=x2y2/(x2+y4)<=x2y2/(x2+0)=y2–>0 när (x,y)—>(0,0)
Varför tar vi just i , och vad händer med i nämnaren? Är syftet här att hitta en övre gräns som "stänger in" vår ursprungliga uttryck, tillsammans med den undre gränsen?
Alltså, genom att visa att:
och att när , kan vi använda instängningssatsen för att dra slutsatsen att:
y4>=0 Genom att ta bort den gör vi nämnaren mindre och bråket större.
Ja, vi får en instängning som löser uppgiften.
Behövs det en instängning här? När y är 0 så är hela uttrycket 0, så gränsvärdet är 0.
Laguna skrev:Gå tillbaka till ursprungsuttrycket och se vad det blir.
Kan man inte stoppa in vinklarna , och i i uttrycket ?
Eller varför behöver man göra det i ursprungliga uttrycket istället? Tänker att jag tar bara förenklade bråket och undersöker värdena.
Hursomhelst, i de "speciella" fallen får vi ‚ och då de är obestämda, vad kan man konstatera om gränsvärdet för ?
Laguna skrev:Behövs det en instängning här? När y är 0 så är hela uttrycket 0, så gränsvärdet är 0.
Instängningen sker då vi säger att . Vi kan inte se gränsvärdet direkt från VL.
Dani163 skrev:Laguna skrev:Gå tillbaka till ursprungsuttrycket och se vad det blir.
Kan man inte stoppa in vinklarna , och i i uttrycket ?
Eller varför behöver man göra det i ursprungliga uttrycket istället? Tänker att jag tar bara förenklade bråket och undersöker värdena.
Hursomhelst, i de "speciella" fallen får vi ‚ och då de är obestämda, vad kan man konstatera om gränsvärdet för ?
Av samma anledningen som vi inte kan stoppa in x=0 i , vi får en division med 0.
Vi måste först skriva om uttrycket så att vi inte får detta problem. Uttrycket du hade från början kommer inte leda till detta problem för de givna värdena på theta (vilket är bra).
Calle_K skrev:Dani163 skrev:Laguna skrev:Gå tillbaka till ursprungsuttrycket och se vad det blir.
Kan man inte stoppa in vinklarna , och i i uttrycket ?
Eller varför behöver man göra det i ursprungliga uttrycket istället? Tänker att jag tar bara förenklade bråket och undersöker värdena.
Hursomhelst, i de "speciella" fallen får vi ‚ och då de är obestämda, vad kan man konstatera om gränsvärdet för ?
Av samma anledningen som vi inte kan stoppa in x=0 i , vi får en division med 0.
Vi måste först skriva om uttrycket så att vi inte får detta problem. Uttrycket du hade från början kommer inte leda till detta problem för de givna värdena på theta (vilket är bra).
Ok, så i början har vi:
,
och när vi stoppar in :
Samt :
Vad gör man härifrån?
Nämnarna blir inte 0.
Calle_K skrev:Laguna skrev:Behövs det en instängning här? När y är 0 så är hela uttrycket 0, så gränsvärdet är 0.
Instängningen sker då vi säger att . Vi kan inte se gränsvärdet direkt från VL.
Vi tittar på just fallet y =0 nu.
Laguna skrev:Calle_K skrev:Laguna skrev:Behövs det en instängning här? När y är 0 så är hela uttrycket 0, så gränsvärdet är 0.
Instängningen sker då vi säger att . Vi kan inte se gränsvärdet direkt från VL.
Vi tittar på just fallet y =0 nu.
Ok, i sådant fall behöver vi inte instängning.
Men vill vi använda Tomtens metod generellt (inte omvandla till polära koordinater) behöver vi använda instängning.
Dessutom finns det väl ingen anledning att särbehandla fallet y=0? Detta hanteras i den generella instängningen.
Calle_K skrev:Nämnarna blir inte 0.
Nej precis, jag redigerade mitt inlägg. Men här slutar vi upp med en obestämd form (0/0), vad gör man då? Kör man L'Hôpitals regel?
Försöker lära mig att lösa uppgiften via denna metod då det kan vara behändigt att kunna båda metoderna.
Dani163 skrev:Calle_K skrev:Nämnarna blir inte 0.
Nej precis, jag redigerade mitt inlägg. Men här slutar vi upp med en obestämd form (0/0), vad gör man då? Kör man L'Hôpitals regel?
Försöker lära mig att lösa uppgiften via denna metod då det kan vara behändigt att kunna båda metoderna.
I slutändan får du helt enkelt att
Du kan jämföra detta med att täljaren går mot 0 oändligt snabbare (eftersom att den redan är 0) jämfört med nämnaren som går mot 0 i linjär takt. Skulle vi t.ex. ha i täljaren skulle också gränsvärdet gå mot 0 eftersom att täljaren går mot 0 kvadratiskt, vilket är snabbare än linjärt.
Calle_K skrev:Laguna skrev:Calle_K skrev:Laguna skrev:Behövs det en instängning här? När y är 0 så är hela uttrycket 0, så gränsvärdet är 0.
Instängningen sker då vi säger att . Vi kan inte se gränsvärdet direkt från VL.
Vi tittar på just fallet y =0 nu.
Ok, i sådant fall behöver vi inte instängning.
Men vill vi använda Tomtens metod generellt (inte omvandla till polära koordinater) behöver vi använda instängning.
Dessutom finns det väl ingen anledning att särbehandla fallet y=0? Detta hanteras i den generella instängningen.
Så kan man göra, men du själv skrev i inlägg #2 att vi hade kvar specialfallen, och Dani163 frågade varför.
Laguna skrev:Calle_K skrev:Laguna skrev:Calle_K skrev:Laguna skrev:Behövs det en instängning här? När y är 0 så är hela uttrycket 0, så gränsvärdet är 0.
Instängningen sker då vi säger att . Vi kan inte se gränsvärdet direkt från VL.
Vi tittar på just fallet y =0 nu.
Ok, i sådant fall behöver vi inte instängning.
Men vill vi använda Tomtens metod generellt (inte omvandla till polära koordinater) behöver vi använda instängning.
Dessutom finns det väl ingen anledning att särbehandla fallet y=0? Detta hanteras i den generella instängningen.
Så kan man göra, men du själv skrev i inlägg #2 att vi hade kvar specialfallen, och Dani163 frågade varför.
Det finns 2 olika lösningsmetoder.
Antingen använder vi oss av polära koordinater som jag förespråkat. Det leder till att vi måste behandla specialfallen theta=pi/2 och theta=3pi/2, vilket Dani163 gör i inlägg #12. Han gör detta mha polära koordinater men det går även bra att översätta vinkeln till kartesiska koordinater, i sådant fall fixerar vi x=0 och undersöker gränsvärdet då y går mot 0.
Den andra metoden (instängnings) är den som Tomten lagt fram. För den behöver vi inte några specialfall utan kan behandla allt generellt mha av instängning
Tomtens slagkraftiga one-liners till lösningar betonar verkligen enkelheten hos instängningsmetoden, men jag tycker ändå att polär form är det mest intuitiva sätt att förstå 2-dimensionella gränsvärden.
Man även studera uttrycket för godt. rät linje y=kx (inkl. x=0).
Trinity2 skrev:Man även studera uttrycket för godt. rät linje y=kx (inkl. x=0).
Men då har man kvar möjligheten att gränsvärdet är något annat om man närmar sig t ex längs en andragradskurva.
Smaragdalena skrev:Trinity2 skrev:Man även studera uttrycket för godt. rät linje y=kx (inkl. x=0).
Men då har man kvar möjligheten att gränsvärdet är något annat om man närmar sig t ex längs en andragradskurva.
På vilket sätt skulle det ske? Uttrycket blir då
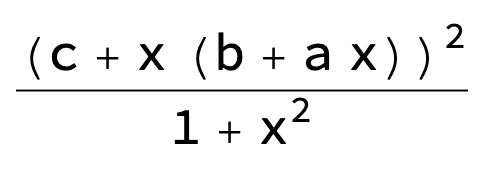
och jag ser inte hur skulle bli annat än 0 då c=0 då kurvan går genom origo.
Om man visar att gränsvärdet blir samma längs alla räta linjer har man ändå inte bevisat att gränsvärdet blir samma längs alla tänkbara vägar. Jag säger inte att gränsvärdet inte är samma, bara att man inte har visat det!
Smaragdalena skrev:Om man visar att gränsvärdet blir samma längs alla räta linjer har man ändå inte bevisat att gränsvärdet blir samma längs alla tänkbara vägar. Jag säger inte att gränsvärdet inte är samma, bara att man inte har visat det!
En rät linje genom origo är en radie och kan representeras av polära koordinater…och vi är tillbaka enligt ovan, på ett annat sätt.
PROBLEM!
Det visar sig att användning av polära koordinater faktiskt inte är så effektivt som jag trodde. Efter lite efterforskning så verkar det helt enkelt vara lite klurigt att använda denna metod; den fungerar om det finns ett gränsvärde, men inte om gränsvärdet saknas, vilket gör det poänglöst att använda denna för att försöka bevisa existensen av något gränsvärde.
Felet jag gjorde i denna tråd var att anta att vinkeln är konstant. Detta medför att vi egentligen undersöker gränsvärdet längs räta linjer vilket Trinity2 påpekade, och mycket riktigt som Smaragdalena säger så kommer inte detta bevisa existens av gränsvärdet. Det vi måste göra istället är att låta vinkeln vara en variabel som beror av r.
LÖSNING?
Om vi kan begränsa skillnaden mellan uttrycket och gränsvärdet med en funktion som enbart beror på r kan vi säga att gränsvärdet faktiskt existerar. I vårt fall har vi , för någon funktion g(r).
Vi kan skriva om uttrycket till , detta uttryck kan begränsas med vilket går mot 0 då r->0.
Dock kräver vi att vi känner till gränsvärdet för att denna metod ska fungera, och då blir det som sagt poänglöst att försöka bevisa existensen (Annars kan man försöka gissa gränsvärdet?). Polära koordinater kan användas för att motbevisa existens, vill du däremot bevisa existensen visar det sig nog att Tomtens instängningsmetod funkar bättre.
Lite läsning:
StackExchange - Användning av polära koordinater för att bevisa existens av gränsvärden i 2D
StackExchange - Motexempel där polära koordinater inte räcker till
Tillägg: 23 jun 2024 22:57
Det går bra att påbörja en lösning mha polära koordinater. Om uttrycket, efter förenkling, inte beror på vinkeln (eller mer generellt är begränsad av en funktion som inte beror på vinkeln) kan vi bestämma gränsvärdet. Detta var fallet i din tidigare tråd.




