Lösa ekvationer med sinus och cosinus
När man ska lösa 5cos2x+3sinx-4=0 då väljer man som enligt bilden att subtrahera 3sin2x och INTE dividera. För då kan man förlora lösningar vilket man gör i detta fall om man gör det. När kan man förlora lösningar? Är det om man dividerar med sinus eller cosinus endast eller gäller det även om man skulle förenkla och dividera med 10 exempelvis. Dessutom finns det andra sätt att råka "förlora" en lösning alltså missa den när man förenklar?
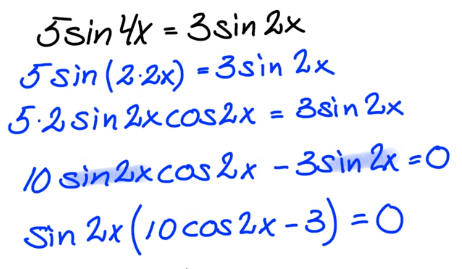
Det gäller att inte dividera med i VL och HL, då kan man tappa lösningar. t.ex. när .
Att dela med är däremot riskfritt.
När du skriver "dividera med 0 i VL och HL" menar du att förkorta med 0 eller menar du att när ett led är 0 så kan man inte dividera med sinus eller cosinus men med t.ex. ett tal som 10 går bra.
Det finns andra uttryck som också kan ha värdet 0, t ex 1-x^2. Då måste man också vara försiktig.
Arbetsmyran skrev:När du skriver "dividera med 0 i VL och HL" menar du att förkorta med 0 eller menar du att när ett led är 0 så kan man inte dividera med sinus eller cosinus men med t.ex. ett tal som 10 går bra.
Det är det första jag menar. I det här fallet är dividera = förkorta.
Varför kan man dividera här (bilden nedan) med cosinus utan att förlora lösningar, men det går inte att dividera med sinus i uppgiften ovan för då förlorar man lösningar. Vad är skillnaden? Båda löser man en ekvation med sinus och cosinus.
cos(x) är en faktor i alla termer i vänsterledet.
Om cos(x) hade varit noll så hade vänsterledet blivit noll, men vi får veta att det är 1. Alltså kan cos(x) inte vara noll.
Jag fattar inte riktigt, kan du typ ge ett exempel eller rita en pil på hur du menar?
Om cos(x) gånger något blir 1, så är det helt omöjligt att cos(x) är noll.
I första uppgiften, så om man dividerar 3sin2x med sig själv då blir det också 1 så jag fattar inte riktigt hur du menar.
Bilden i ditt första inlägg har ingen division.
Nej, men om gör utför en division istället för den subtraktion du ser i bilden så försvinner lösningar, man får några men inte alla. Men jag fattar inte hur divisionen tar bort lösningar.
Arbetsmyran skrev:Nej, men om gör utför en division istället för den subtraktion du ser i bilden så försvinner lösningar, man får några men inte alla. Men jag fattar inte hur divisionen tar bort lösningar.
Vi förenklar det så att det blir tydligt.
Tänk dig att du har en ekvation som lyder A•B = 0.
Du vet (enligt nollproduktmetoden) att denna ekvation har de två lösningarna A = 0 och B = 0.
Men om du (istället för att använda nollproduktmetoden) dividerar båda sidor med A så får du ekvationen B = 0, med lösning B = 0.
Du har alltså tappat bort lösningen A = 0.






