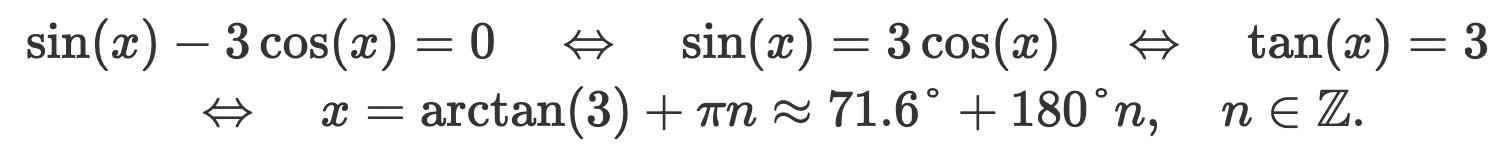Lösa ekvation
Hej jag förstår inte varför min metod är fel ?? Enligt facit så ska man skriva om det till en tan funktion och då får man bara 1 svar som är x=72+180*n
varför ger min metod 2 svar och fel period ???

Dina svar är rätt. Tänk på att .
Fall 1 ger lösningarna:
osv
Fall 2 ger lösningarna:
osv
Kollar vi på facit, alltså får vi
osv
De beskriver samma sak, facit har bara slagit ihop de två fallen till ett fall. Det kan vi göra eftersom graderna skiljer sig exakt med
AlexMu skrev:Dina svar är rätt. Tänk på att .
Fall 1 ger lösningarna:
osv
Fall 2 ger lösningarna:
osv
Kollar vi på facit, alltså får vi
osv
De beskriver samma sak, facit har bara slagit ihop de två fallen till ett fall. Det kan vi göra eftersom graderna skiljer sig exakt med
Slår man alltid ihop lösningarna när det handlar om cos(x+v) = 0 och sin(x+v)=0 ??
ger att
eller . Så ja, det borde väl bli så?
(Hoppas det är ok att jag använder radianer istället för grader)
AlexMu skrev:
ger att
eller . Så ja, det borde väl bli så?
(Hoppas det är ok att jag använder radianer istället för grader)
Lite enklare:
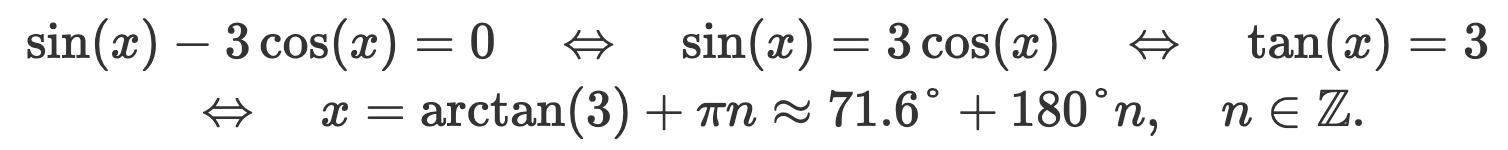
Trinity2 skrev:AlexMu skrev:
ger att
eller . Så ja, det borde väl bli så?
(Hoppas det är ok att jag använder radianer istället för grader)Lite enklare:
Antog att detta är vad de gjorde i facit eftersom de nämner att det användes en tan funktion i lösningen