Lösa differentialekvation med potensserier
Hej, behöver hjälp med att lösa denna uppgift. Har svårt med potensserier och hur man ska bemöta dessa problem. Jag ska lösa följande differentialekvation mha potensserier,
Har jag gjort följande, vet inte om det är en korrekt början på lösningen och hur jag ska gå vidare.
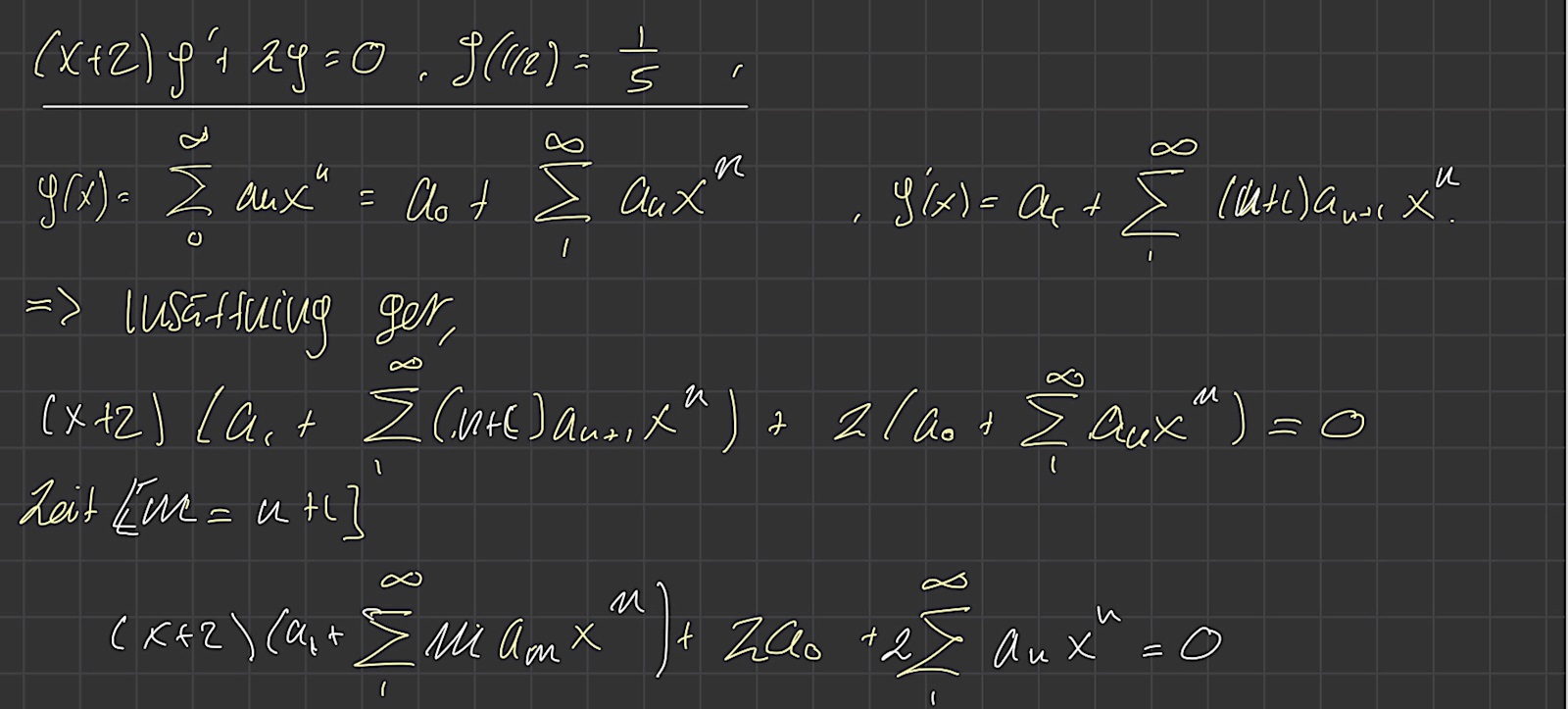
Tacksam för hjälp!
Utveckla multiplikationen med x+2 och bilda sedan ett uttryck för koefficienten för xn. Sätt dessa till noll.
Menar du likt följande? Kan definiera a_0 eller a_1 men vad säger det mig? Hur får jag med bivilkoret? Till serien, vet jag inte heller hur man ska fortsätta? 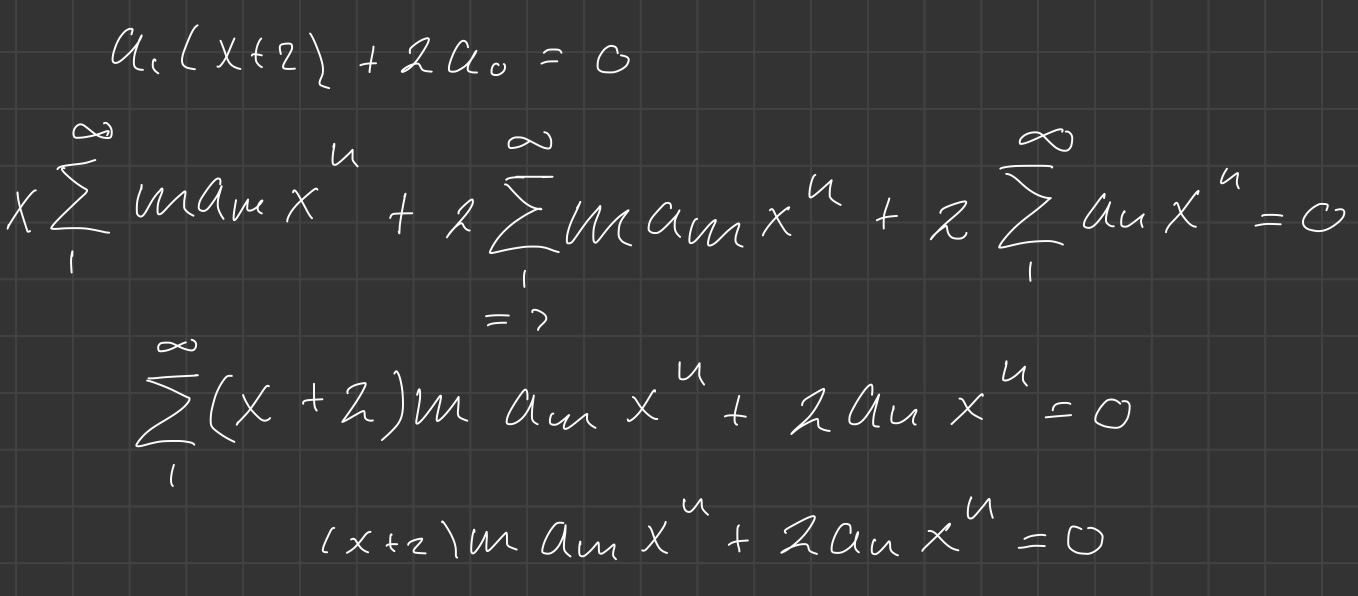
Vad får xn för koefficient?
Antar att man kan formulera det vidare soml,
men det är kanske inte det du menar?
Om du utvecklar det uttrycket får du en xn+1 också. Samla alla xn och inga andra.
Likt detta? Eller menade du även x+1 termen?
Låt oss prova med konkreta potenser. Sätt in a0+a1x+a2x2, hur blir det då?
Eller är det något jag har missuppfattat?


