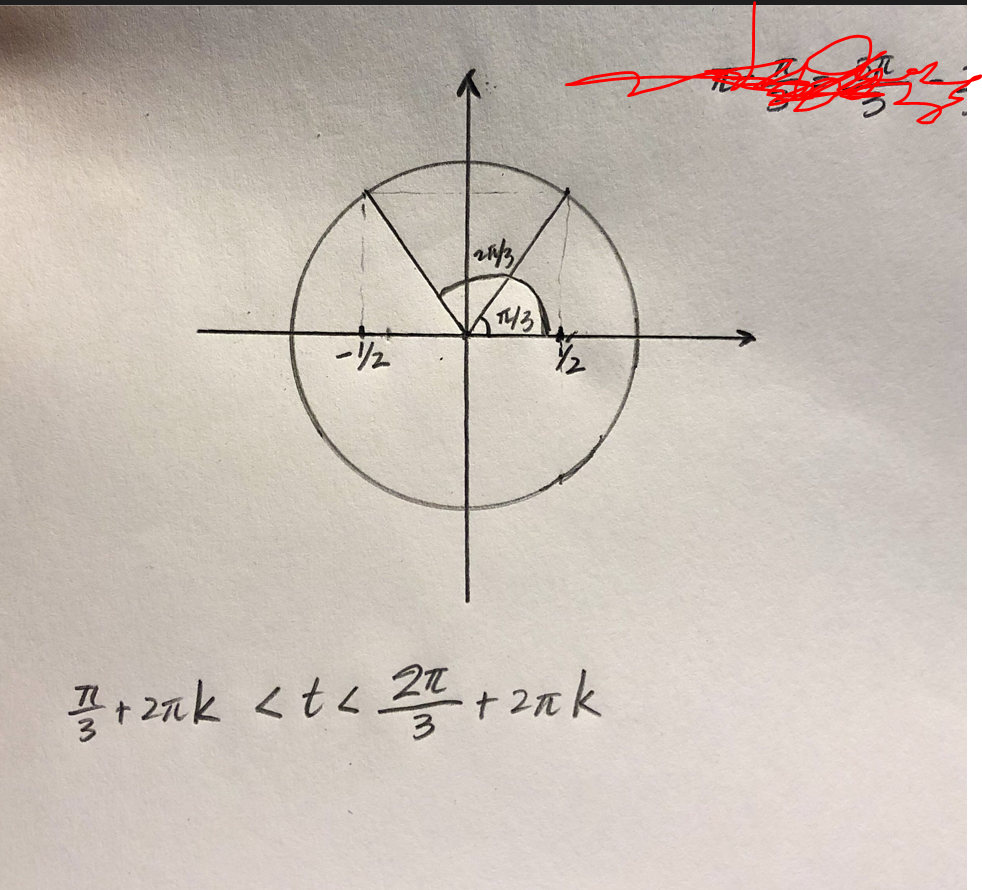
Lös olikeheten (innehåller trigonometriska ekvation)
Jag behöver hjälp med denna uppgiften.
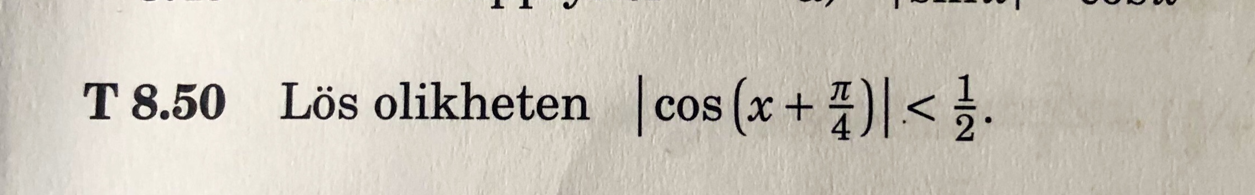
Tips från boken:

Min försök:


Facit:
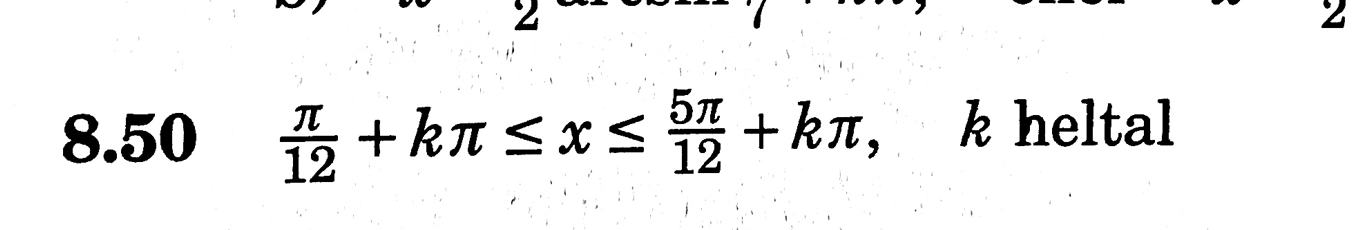
Jag hänger inte med på vad det är du gör - du behöver använda fler ord för att det skall gå att förstå hur du tänker.
Börja med att komplettera din enhetscirkel så att den visar |cos(t)|<½. Lägg upp bilden här.
Smaragdalena skrev:Börja med att komplettera din enhetscirkel så att den visar |cos(t)|<½. Lägg upp bilden här.
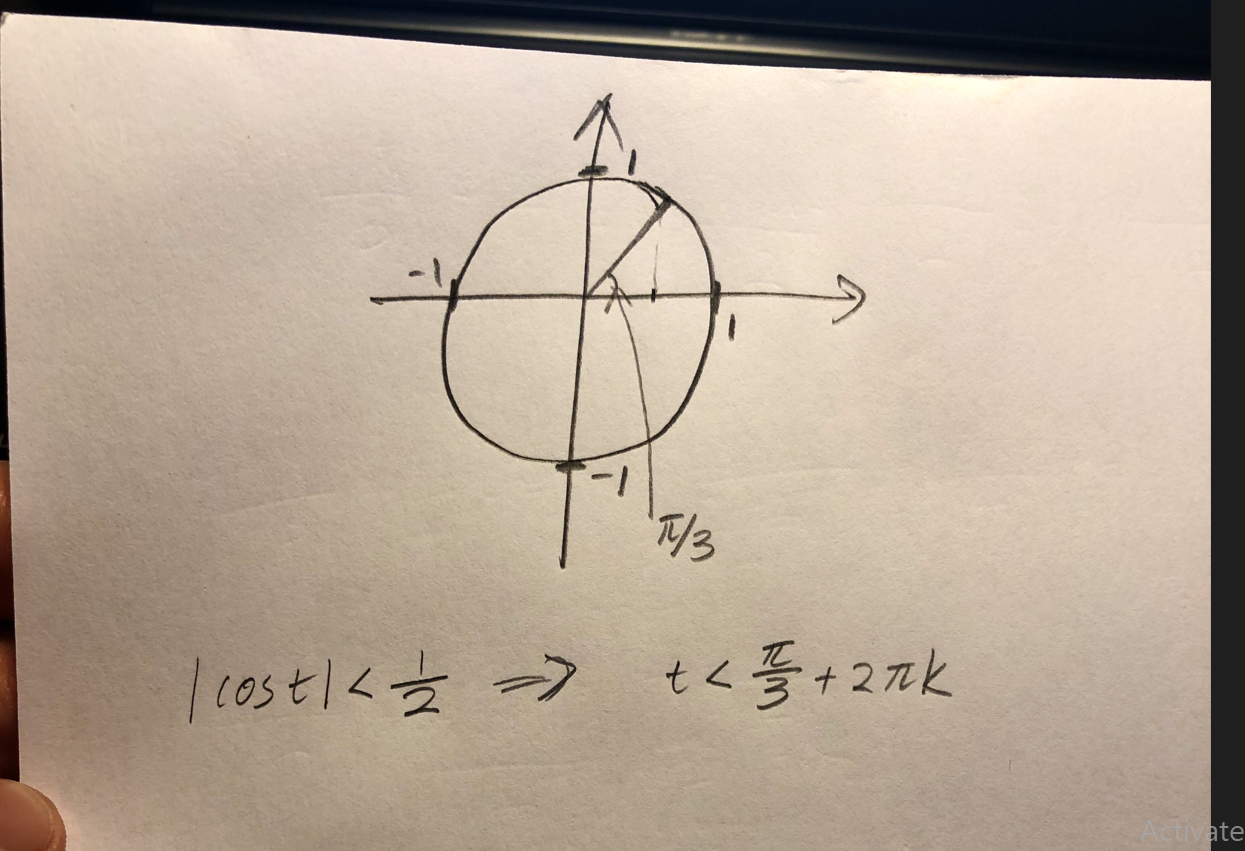
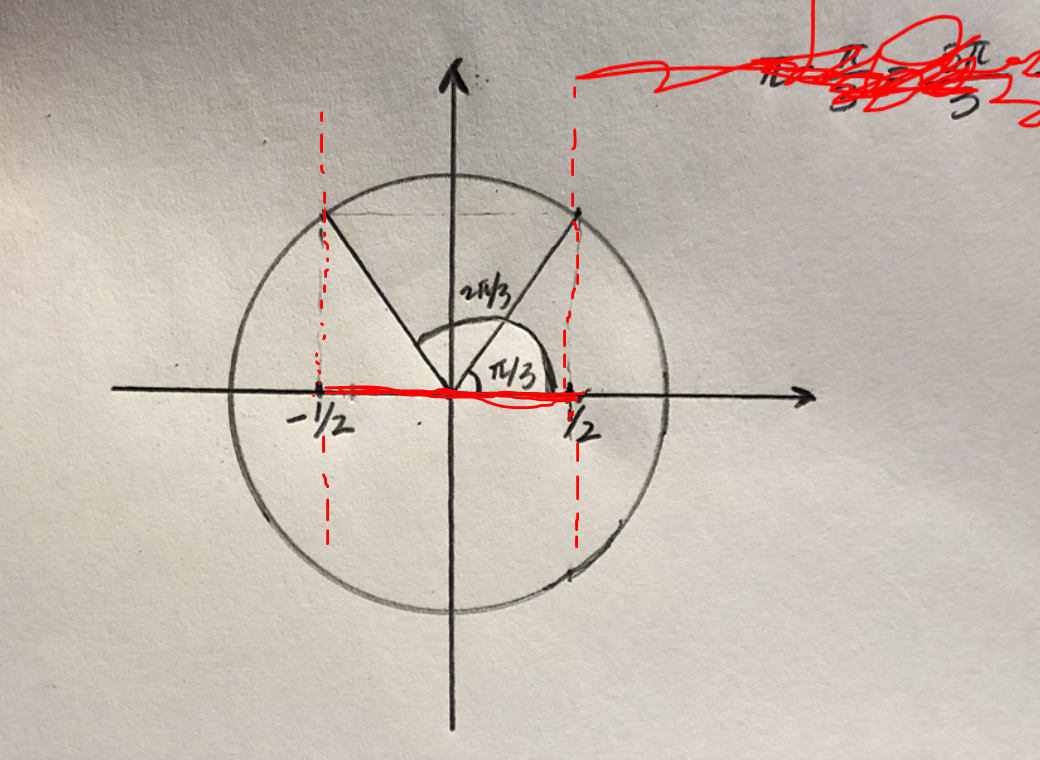
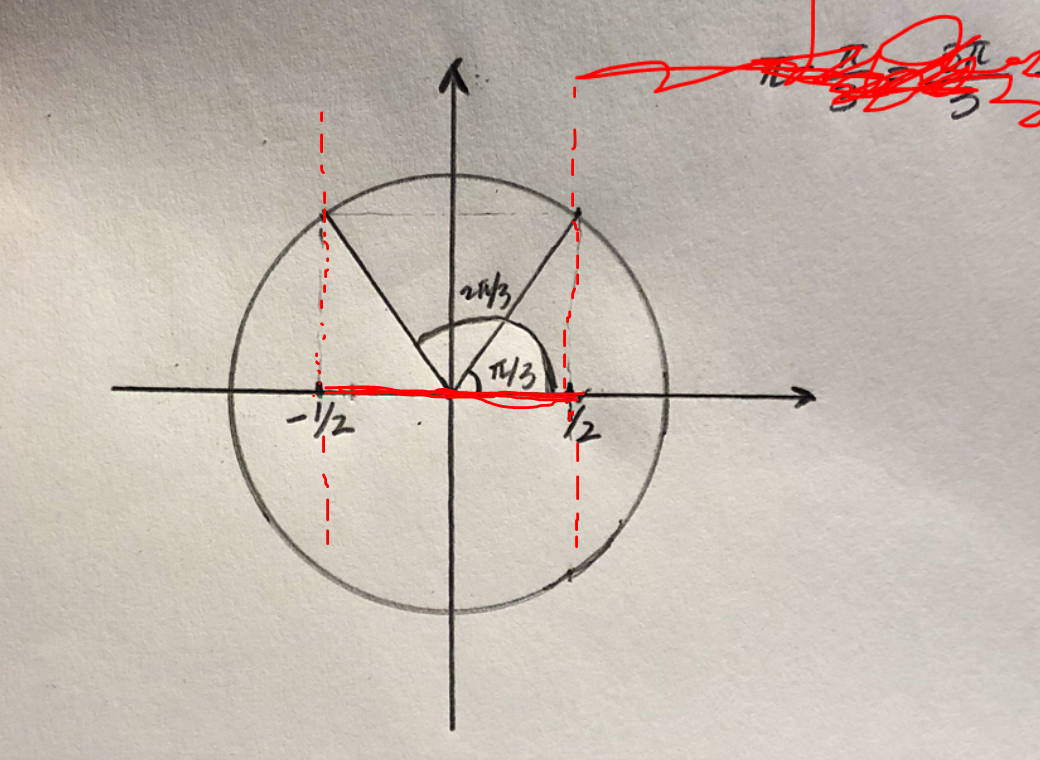
Rita in att |cos(t)| < ½, d v s rita in linjerna x= ½ och x = -½ i bilden med enhetscirkeln. Lägg upp den nya bilden.
För tredje gången: Rita in de båda lodräta linjerna! Du behöver ha en korrekt bild innan vi kan fortsätta. Så som det är nu har du bara ritat in hälften av lösningarna.
Jag har redan ritat två bilder, hur ser den "korrekta bilden" i din hjärnan?
Du får visar.
Du har fortfarande inte ritat in linjerna x = 0,5 och x = -0,5 i enhetscirkeln. Gör det och lägg upp bilden! Linjerna skall inte ta slut vid y = 0.
Marcus N skrev:Jag har redan ritat två bilder, hur ser den "korrekta bilden" i din hjärnan?
Du får visar.
På samma sätt som t.ex. y = 3 är en horisontell linje som ligger 3 l.e. ovan x-axeln så är t.ex. x = 5 en vertikal linje som ligger 5 l.e. till höger om y-axeln.
Smaragdalena skrev:Du har fortfarande inte ritat in linjerna x = 0,5 och x = -0,5 i enhetscirkeln. Gör det och lägg upp bilden! Linjerna skall inte ta slut vid y = 0.
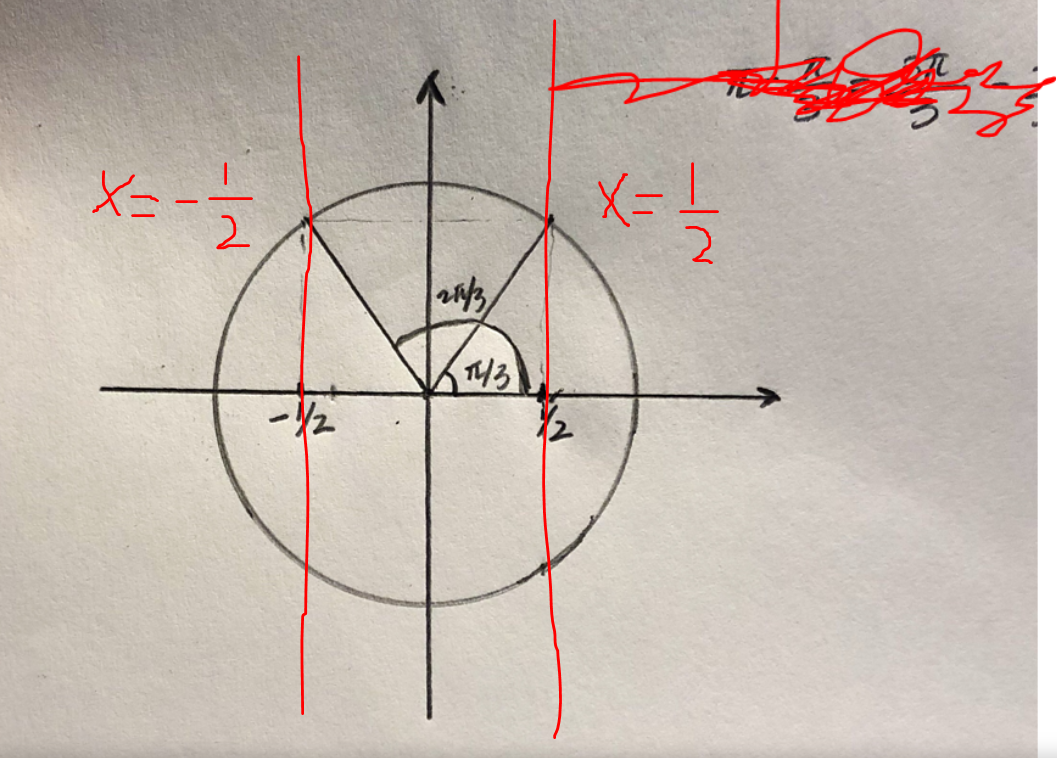
Bra!
Ser du nu att det finns ytterligare ett intervall av vinklar t som uppfyller villkoret |cos(t)| < 1/2?
Vilken intervall är det?
Tänk på att cosinusvärdet av en vinkel är lika med den horisontella koordinaten för den av vinkeln utpekade punkten på enhetscirkeln.
Du letar alltså efter alla punkter på enhetscirkeln som har en horisontell koordinat som ligger mellan -1/2 och 1/2.
Kan du markera alla dessa områden på enhetscirkeln?
Menar du den här området eller?
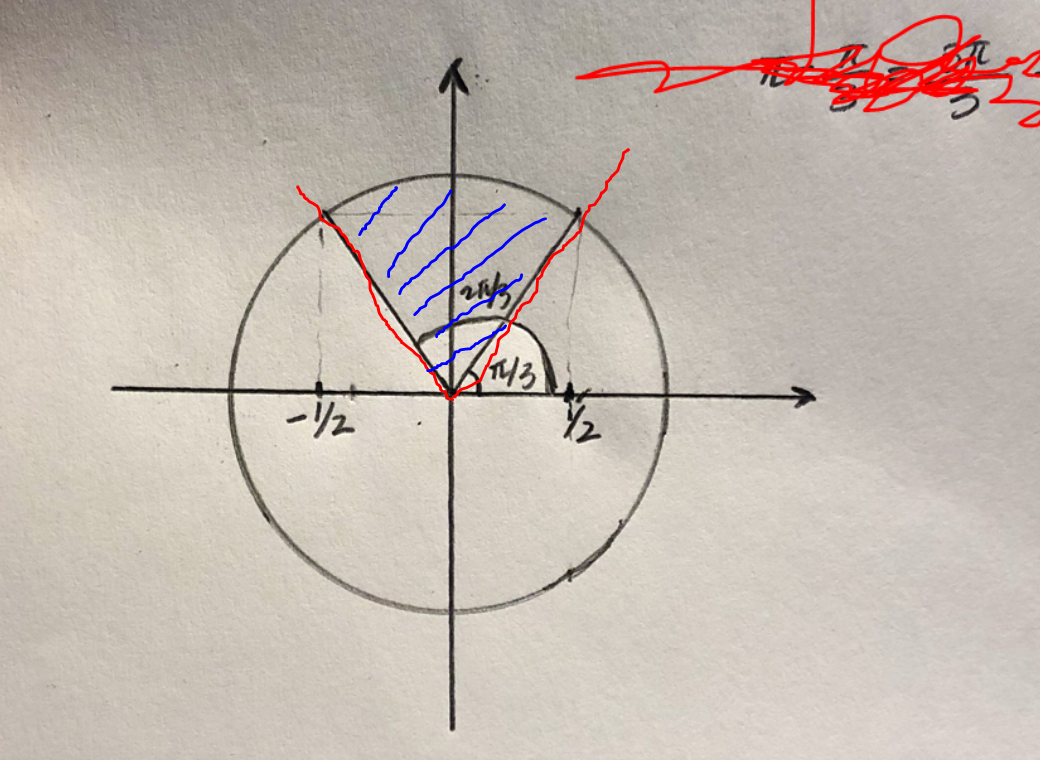
Nej.
- Det är bara punkterna på cirkeln (dvs på cirkelskivans rand) som du är ute efter.
- Det finns fler punkter på cirkeln som har en horisontell koordinat mellan -1/2 och 1/2. Notera att cirkeln går ett helt varv. Här får du hjälp av den bild du ritade i svar #10.
Yngve skrev:Nej.
- Det är bara punkterna på cirkeln (dvs på cirkelskivans rand) som du är ute efter.
Här är alla punkter på cirkel skivans rand:
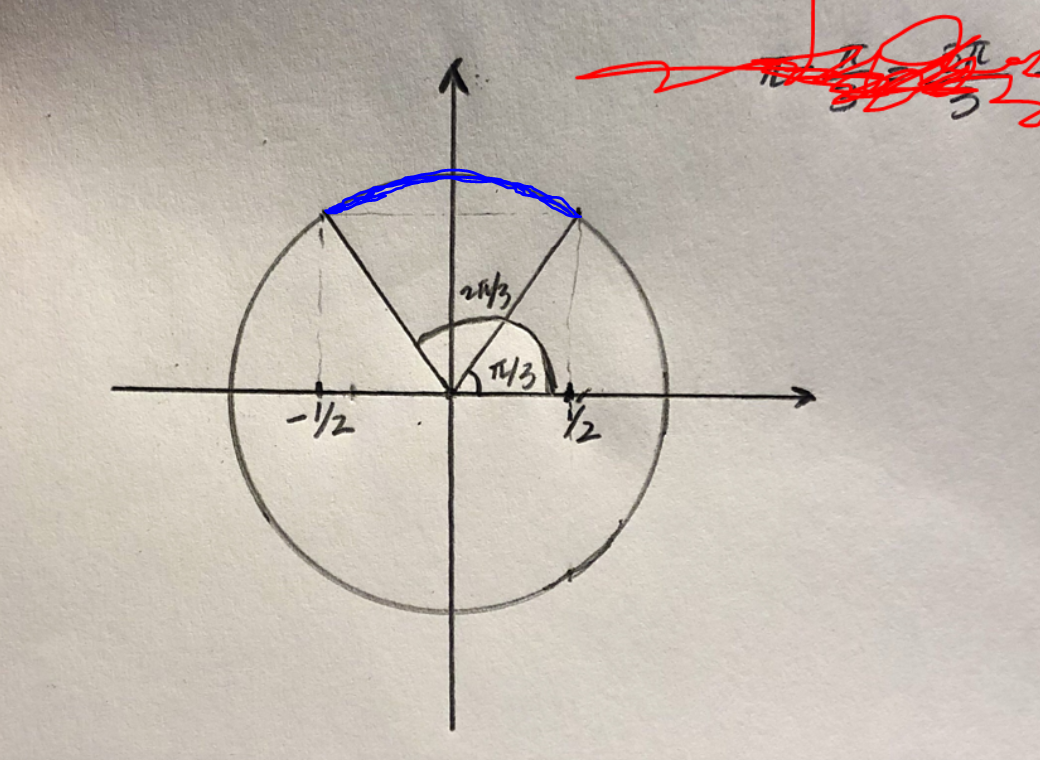
Bra så långt,men nu har jag fått in ett klagomål som lyder:
Men hallå där Markus N.
Ignorerar du oss?
Vi finns faktiskt!
Hälsningar från "Alla punkter i kvadrant 3 och 4"
Yngve skrev:Nej.
- Det finns fler punkter på cirkeln som har en horisontell koordinat mellan -1/2 och 1/2. Notera att cirkeln går ett helt varv. Här får du hjälp av den bild du ritade i svar #10.
Och här är alla horisontell korrdinat mellan -1/2 och 1/2
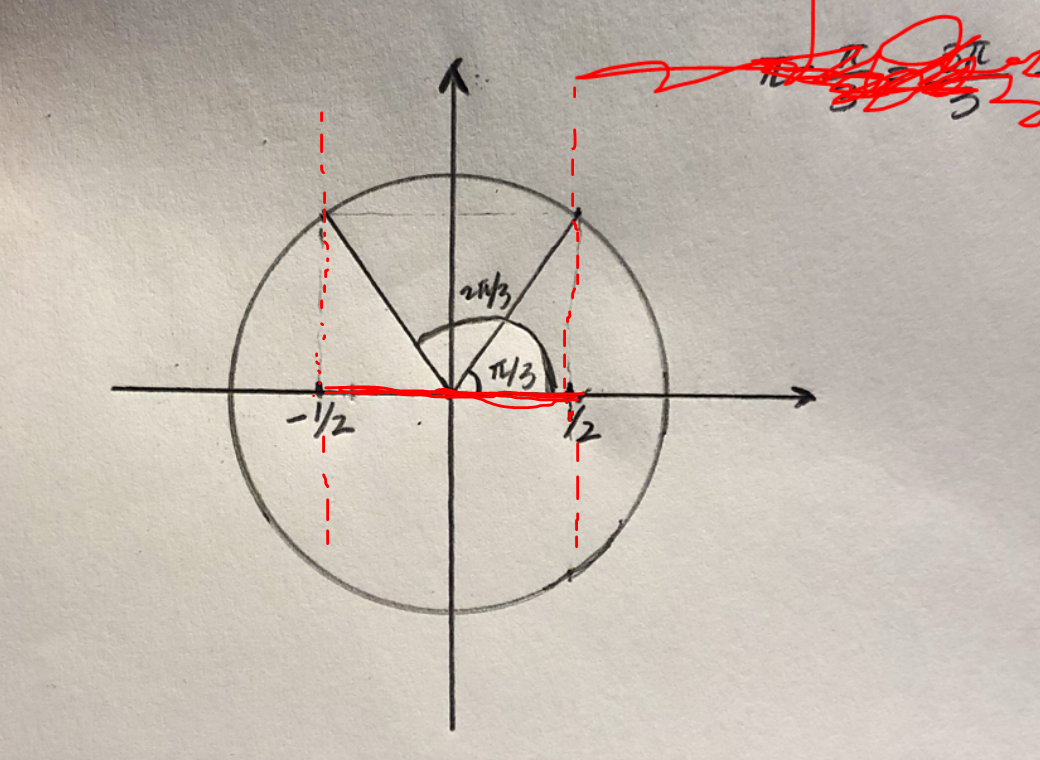
Marcus N skrev:
Ja, och nu vill jag att du markerar alla punkter på cirkeln som har samma horisontella koordinater som de du har markerat med rött.
Notera att cirkeln går ett helt varv. Här får du hjälp av den bild du ritade i svar #10.
Om du ändå fastnar kan vi pröva på ett annat sätt.
- Markera med rött alla punkter på hela enhetscirkeln (dvs alla punkter på cirkelskivans rand).
- Markera med blått de av dessa punkter som har en horisontell koordinat som ligger mellan -1/2 och 1/2, dvs markera med blått de av dessa punkter som ligger mellan de vertikala linjerna x = -1/2 och x = 1/2 (från ditt svar #10).
Yngve skrev:Marcus N skrev:
Ja, och nu vill jag att du markerar alla punkter på cirkeln som har samma horisontella koordinater som de du har markerat med rött.
Notera att cirkeln går ett helt varv. Här får du hjälp av den bild du ritade i svar #10.
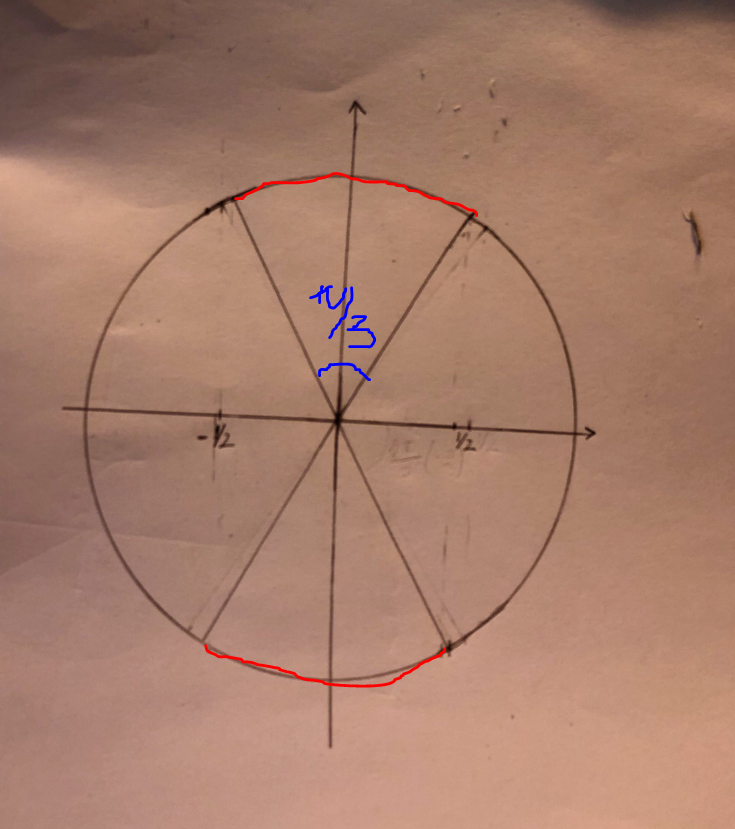
Ja! Nu har du gjort en korrekt figur som visar de två cirkelsegment på enhetscirkeln där olikheten |cos(t)| < 1/2 är uppfylld.
Nästa steg är att beskriva vilka vinklar t som motsvarar dessa röda cirkelsegment.
Hur uttrycka man denna vinkeln?
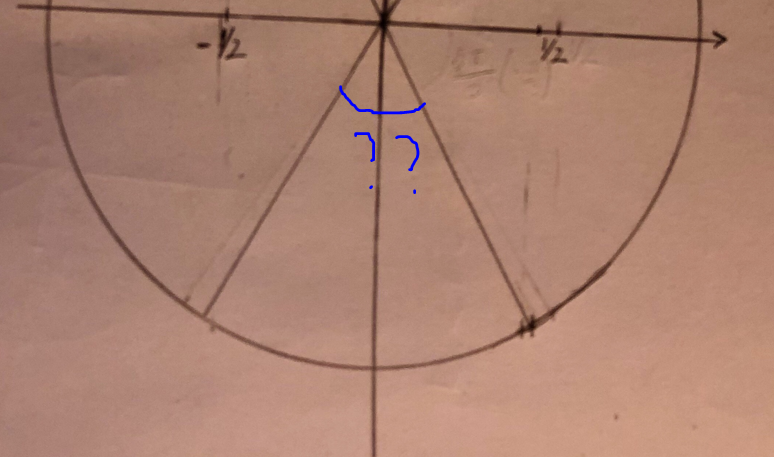
Är det -pi/3 eller?
En av vinklarna är -pi/3. Vilken av dem, och hur stor är den andra vinkeln?
Vinklarna räknas alltid moturs från den positiva delen av den horisontella koordinataxeln.
Du har alltså fyra vinklar a, b, c och d att ta reda på:

t ligger mellan intervall b-a och d-c.
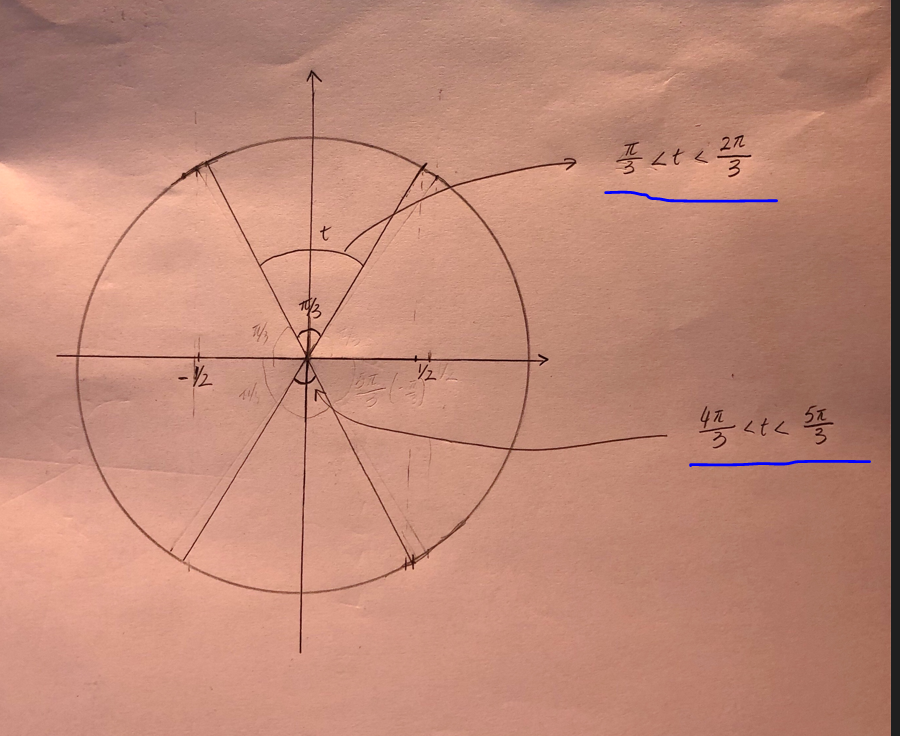
Man kan göra som Yngve skriver, eller man kan räkn a med att de båda "nedersta" vinklarna är negativa. Det är en smaksak.
Men har ja tänkt rätt i #26 eller?
Marcus N skrev:Men har ja tänkt rätt i #26 eller?
Ja det är rätt.
Nu har du två olikheter och du kan ersätta med i dessa för att få ut villkoren för . Detta är lösningen på uppgiften.
Marcus N skrev:
Nej. Vilka vinklar ligger längst till vänster respektive höger för vardera intervallet?
Det är aldrig en bra idé att ha i samband med olikheter, det blir jätterörigt!
Nu är jag helt löst. Jag trode att ja hade rätt i #26! Att t alltså (x+pi/4) ligger mellan (pi/3 , 2pi/3) och (4pi/3 , 5pi/3).
Jag förstår inte den här frågan: "Vilka vinklar ligger längst till vänster respektive höger för vardera intervallet?"
Vilka vinklar tänker du på? Kan du visar med en bild?
Och hur ska du lösa en cos funktion om du inte har med +/- tecken??
Marcus N skrev:Nu är jag helt löst. Jag trode att ja hade rätt i #26! Att t alltså (x+pi/4) ligger mellan (pi/3 , 2pi/3) och (4pi/3 , 5pi/3).
Det har du rätt i, men det du har skrivit i #30 är något helt annat (jag tror att det rätta finns med, men det är så rörigt att jag itne är säker). Du har sammanlagt 2 intervall att undersöka (förutom perioden).
Jag förstår inte den här frågan: "Vilka vinklar ligger längst till vänster respektive höger för vardera intervallet?"
Vilka vinklar tänker du på? Kan du visar med en bild?
Och hur ska du lösa en cos funktion om du inte har med +/- tecken??
Du får väldigt många intervall att undersöka om du skall ha överallt.
Jag förstår inte varför #30 är fel, kan du vara lite mer specifikt än bara säga"det du skriver i #30 är något helt annat".
Vad är den korrekta sätta att skriva olikheten? Om mitt sätt är fel.
Och glöm inte vi måste ta hänsyn till att det är en cos-funktion som ska lösas, så +/- tecken måste vara med på nåt vis. Hur vill du att jag lösa det då?
Marcus N skrev:Vad är den korrekta sätta att skriva olikheten? Om mitt sätt är fel.
Om du ska begränsa lösningsmängden till endast vinklar i intervallet så är följande olikheter korrekta:
< <
< <
Om du däremot vill ha alla möjliga värden på så måste du lägga till som du har gjort.
Men ska inte vara där.
Och glöm inte vi måste ta hänsyn till att det är en cos-funktion som ska lösas, så +/- tecken måste vara med på nåt vis. Hur vill du att jag lösa det då?
Du har redan tagit hänsyn till genom att du tog med intervallet i kvadrant 3 och 4 (se f.ö. Smaragdalenas svar #27).
Nu blir ja ännu mer förvirrad !
Vad är skillnad mellan dessa olikheterna du har skrivit och dem jag ha skrevt i #30?
Är det bara man får inte ha med +/- när man beräkna olikheter?
Börja med att begränsa dig till vinklar mellan noll och 2pi (eller mellan -pi och pi)
När du har kommit så långt kan du lägga till N hela varv,
Marcus N skrev:Vad är skillnad mellan dessa olikheterna du har skrivit och dem jag ha skrevt i #30?
Skillnaden är att det står ± i den ena men inte i den andra.
Är det bara man får inte ha med +/- när man beräkna olikheter?
Jovisst får du det, men det blir väldigt otydligt vad det är som avses och oftast blir det inte heller rätt.
Exempel:
3 < x < 5 kan ju se tydligt och bra ut, men om vi tittar närmare på vad det egentligen betyder så är det "plus eller minus 3 är mindre än x, som är mindre än plus eller minus 5".
Det betyder alltså att x ska uppfylla alla följande olikheter:
3 < x < 5
3 < x < -5
-3 < x < 5
-3 < x < -5
Du ser hur tokigt det blir.