Lös ekvationen z^3=w
Lös ekvationen då
presentera rötterna grafiskt.
Jag har skrivit om ekvationen i polär form och fått fram de tre lösningarna. Hur presenterar jag de grafiskt? är det i ett komplext talplan? där jag ritar ut vektorerna?
Precis! Placera ut lösningarna i en av dessa (varning för ful konst):
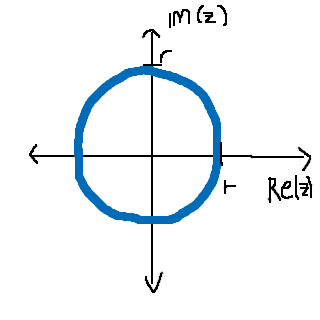
Alla lösningar kommer att hamna på cirkelranden, och du kommer att märka ett mönster i hur de ligger. :)
I det komplexa talplanet, och se till att det syns att de tre rötterna ligger på en cirkel.
Smaragdalena skrev:I det komplexa talplanet, och se till att det syns att de tre rötterna ligger på en cirkel.
Har jag fått rätt när jag får
tycker att de hamnar på en cirkel i det komplexa talplanet!
Nja, det ser inte riktigt rätt ut. om z = -1, kommer inte att ha någon imaginärdel, så det kan inte stämma. Borde det inte bli:
(Plus n*120 grader)?
Smutstvätt skrev:Nja, det ser inte riktigt rätt ut. om z = -1, kommer inte att ha någon imaginärdel, så det kan inte stämma. Borde det inte bli:
(Plus n*120 grader)?
Men hur får jag fram vad cos 20 och sin 20 är? är 20 grader
När man multiplicerar tre (z*z*z) komplexa tal, multipliceras beloppen (1*1*1=1) och adderas vinklarna
Affe Jkpg skrev:När man multiplicerar tre (z*z*z) komplexa tal, multipliceras beloppen (1*1*1=1) och adderas vinklarna
Då får jag alltså
z1 = cos 20 + i sin 20
z2= cos 140 + i sin 140
z3= cos 260 + i sin 260
Men hur skriver jag om dessa i formen z=a+bi?
angelicamaja skrev:Affe Jkpg skrev:När man multiplicerar tre (z*z*z) komplexa tal, multipliceras beloppen (1*1*1=1) och adderas vinklarna
Då får jag alltså
z1 = cos 20 + i sin 20
z2= cos 140 + i sin 140
z3= cos 260 + i sin 260
Men hur skriver jag om dessa i formen z=a+bi?
Uppgiften var väl att presentera rötterna grafiskt?
Har du provat kalkylatorn för att beräkna cos() och sin()?
angelicamaja skrev:
Då får jag alltså
z1 = cos 20 + i sin 20
z2= cos 140 + i sin 140
z3= cos 260 + i sin 260
Men hur skriver jag om dessa i formen z=a+bi?
Det verkar onödigt krångligt att skriva om de komplexa talen på rektangulär form.
Utnyttja istället fördelarna med polär form.
Du vet avstånden från origo (beloppen) och vinklarna mot den positiva reella axeln (argumenten).
Det räcker utmärkt för att ungefärligt pricka in de komplexa talen i det komplexa talplanet.
Se det allra första svaret från Smutstvätt.





