lös ekvationen x^(3)+5x^(2)+8x+6
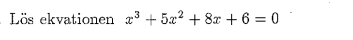

Jag tänker lösa uppgiften ovan som uppgiften nedan för jag förstår bäst hur uppgiften nedan fungerar för fråga efter lös ekvationen.
Kan säga svaret till uppgiften ovan är (x+3)*(x+1)*(x+1) med på att x2=-1 och x3=-1.?
En fråga till varför kom -1 ifrån den står till om (x+1)^(2)=-1 ?

abid skrev:
Jag tänker lösa uppgiften ovan som uppgiften nedan för jag förstår bäst hur uppgiften nedan fungerar för fråga efter lös ekvationen.
Kan säga svaret till uppgiften ovan är (x+3)*(x+1)*(x+1) med på att x2=-1 och x3=-1.?
En fråga till varför kom -1 ifrån den står till om (x+1)^(2)=-1 ?
x= -1 är inte en rot, se nedan
(x+3)*(x+1)*(x+1) = x^3+5x^2+7x+3,
däremot
(x+3)(x+1-i)(x+1+i) = x^3+5x^2+8x+6
Din lösning är alltså rätt
En fråga till var kom -1 ifrån den står till om (x+1)^(2)=-1 ?
vilka av dem nedan är det rätt då nedan du var otydligt när skrev din lösning är rätt menar du att den är fel > (x+3)*(x+1)*(x+1) = x^3+5x^2+7x+3, att det är istället den är >(x+3)(x+1-i)(x+1+i) = x^3+5x^2+8x+6
x= -1 är inte en rot, se nedan
(x+3)*(x+1)*(x+1) = x^3+5x^2+7x+3,
däremot
(x+3)(x+1-i)(x+1+i) = x^3+5x^2+8x+6
Din lösning är alltså rätt
om ett polynom har nollställena a,b och c så är polynomet
k(x-a)(x-b)(x-c) där k är en godtycklig konstant.
Jag förutsatte att du var bekant med det eftersom frågan är på matte 5 nivå.
Nåväl, rötterna är
x1 = -3
x2 = -1+i
x3 = -1-i
Din fråga från förra inlägget
"En fråga till var kom -1 ifrån den står till om (x+1)^(2)=-1 ?" så är svaret att det vet jag inte.




