Lös ekvationen x^3 + (1 - 2i)x^2 + (2 - 6i)x + (2 - 4i) = 0 om en lösning är x = -1
Jag delade x^3 + (1 - 2i)x^2 + (2 - 6i)x + (2 - 4i) med x + 1, det gav mig ekvationen x^2 -2ix + (2-4i), jag löste den genom pq formeln men fick fel svar. Jag fick i +- roten ur (-3 +4i) medan svaren är 1 + 3i och -1-i. Hur kommer man fram till det?
Skicka din lösning.
mrpotatohead skrev:Skicka din lösning.
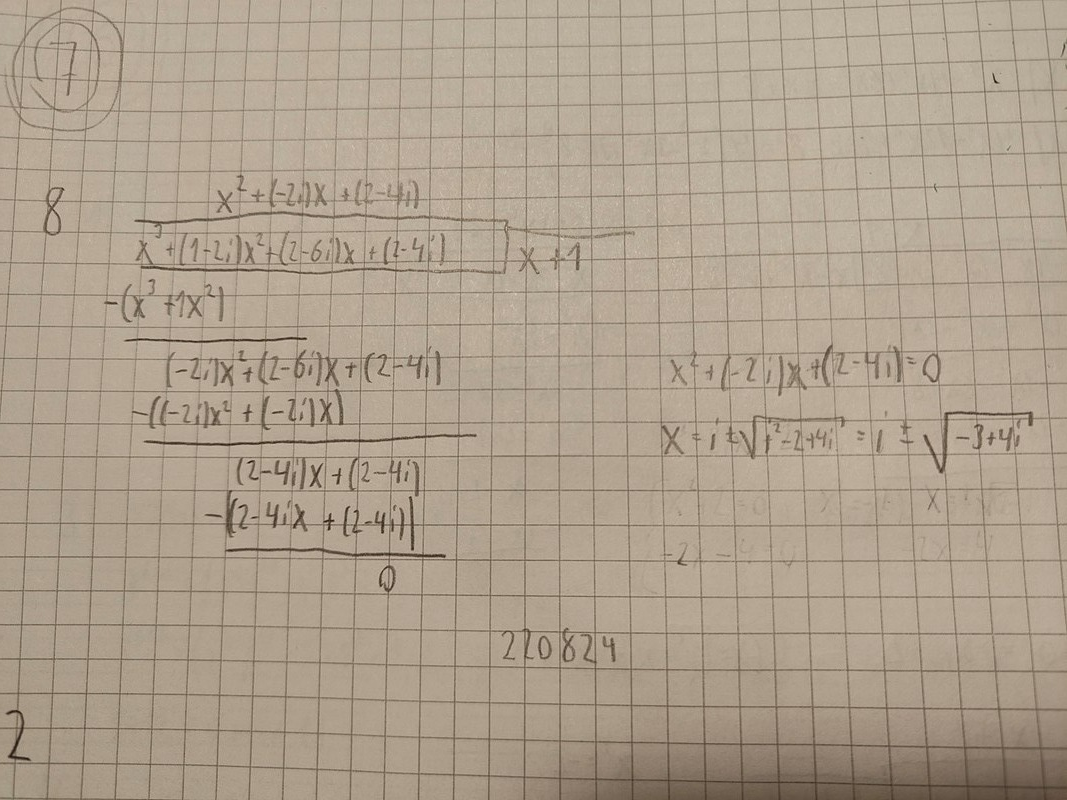
Du får i så fall räkna ut den där roten också. Den visar sig vara 1+2i.
Laguna skrev:Du får i så fall räkna ut den där roten också. Den visar sig vara 1+2i.
Fast det är ju inte möjligt?
Vad får du om du kvadrerar 1+2i?
Laguna skrev:Du får i så fall räkna ut den där roten också. Den visar sig vara 1+2i.
Hur gör man detta utan miniräknare?
Hur gör man detta MED miniräknare?
Om du inte vet hur du ska räkna ut diskriminanten:
a+ib = (-3+4i)0,5
kvadrera bägge led
a2-b2+2abi = -3 + 4i
separera real och imaginärdelarna
a2-b2 = -3
2ab = 4
osv
Smaragdalena skrev:Hur gör man detta MED miniräknare?
Haha, det var kanske en bättre fråga😶🌫️
Finns miniräknare inuti digitala verktyg som löser det fint. Fysiska miniräknare har det svårt..
I just det här fallet blir det snyggt och prydligt om man ritar upp situationen i det komplexa talplanet. Kateterna 3 och 4 borde kännas bekanta.





