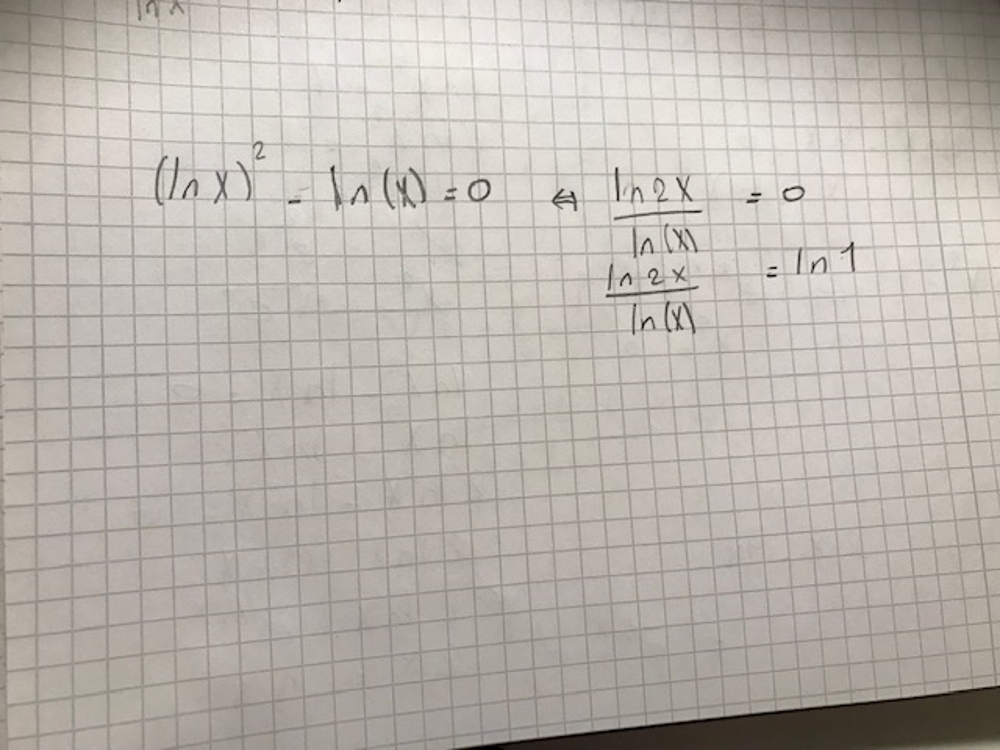lös ekvationen LN

Det stämmer inte, du har tillämpad räkneregler som inte existerar. Det gäller inte att:

$\dfrac{\ln a}{\ln b} = \ln (a-b)$.

Du har en andragradare i $t = \ln x$ så att vi får polynomet:

$f(t) = t^2-t=0$

Prova att faktorisera:

(ln x)^2 - ln x =

ln x * ( lnx -1)

när någon av faktorerna är noll är hela uttrycket 0.

menar du så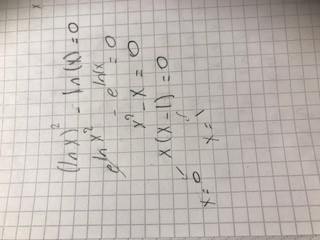

Stämmer, men nu måste vi vara försiktiga och fundera på definitionsmängden för ln(x), vad händer exemeplvis för $x=0$?

då har vi bara en rot x =1. problemet  att facit är  X1= 1, X2= e ??

steg 3 stämmer om $x = \ln x$.

steg två är fel eftersom (lnx)^2 inte är samma sak som ln(x^2).

kan du vara snäll och lösa det?

Blanda inte ihop lnx och x.

Använd tipsen i inlägg #2 eller #3.

nu är den löst, tack för hjälpen!