Lös ekvationen exakt utan räknare
Hej,
har en ekvation jag har lite svårt för. Visar er hur jag försökt räkna fram det:

Vet inte hur jag löser ekvationen riktigt.. ?
Felet du gör är att du gör olika saker i VL och HL här:

Du logaritmerar hela VL men bara delar av HL.
Jag tror att det blir enklare om du istället börjar med att samla alla termer som innehåller x på ena sidan av likhetstecknet, t.ex. genom att dividera båda sidor med 3-x. Eller multiplicera båda sidor med 3x, det ger samma resultat.
Sedan kan du förenkla och logaritmera.
======
Ett annat fel du gör är att du verkar hantera det jag har markerat som att x subtraheras från uttrycket. Det ska istället vara så att uttrycket ska multipliceras med -1. Detta eftersom lg(3-x) är lika med (-x)*lg(3), inte lg(3)-x.

Tack för svaret.
Om jag dividerar så här:
3 ^x / 3 ^-x = 5 * 3 ^-x / 3 ^-x så försvinner 3^-x i H.L men i V.L så behöver jag räkna fram svaret till:
3^x / 3^-x och blir något osäker på hur jag gör det? att dela potenser blir väl : a^x / a^y = a^x-y men om jag redan har - på ena exponenten blir de då:
3^x / 3^-x = 3^x -(-x) = 3 ^x+x = ? vet inte tappar bort mig här
Okej. Men hur kan de här bli exakt när jag får fram massa decimaler.
har gjort så här nu:
 måste lösa uppgiften exakt
måste lösa uppgiften exakt
Att lösa den exakt betyder i detta fallet att du inte räknar ut vad logaritmernas värde blir, utan bara skriver dem som lg(11) eller vad du nu tar logaritmen av. Om din uträkning stämde så vore det exakta svaret 5/3, men att dela med 3 isolerar inte 2x:
okej, men
3^x / 3^-x = 3^x -(-x) = 3^x+x = 3^2x här är de ju klart? hur fick du fram -1 i exponenten? la du till den för att få det rätt i H.L sen? & om så varför görs det inte i H.L med?
Jag tolkade dina uträkningar som:
Men det sista steget stämmer inte, för det blir
Prova igen. Det kanske hjälper att skriva som . Nästa steg är inte en division.
Typ så här?
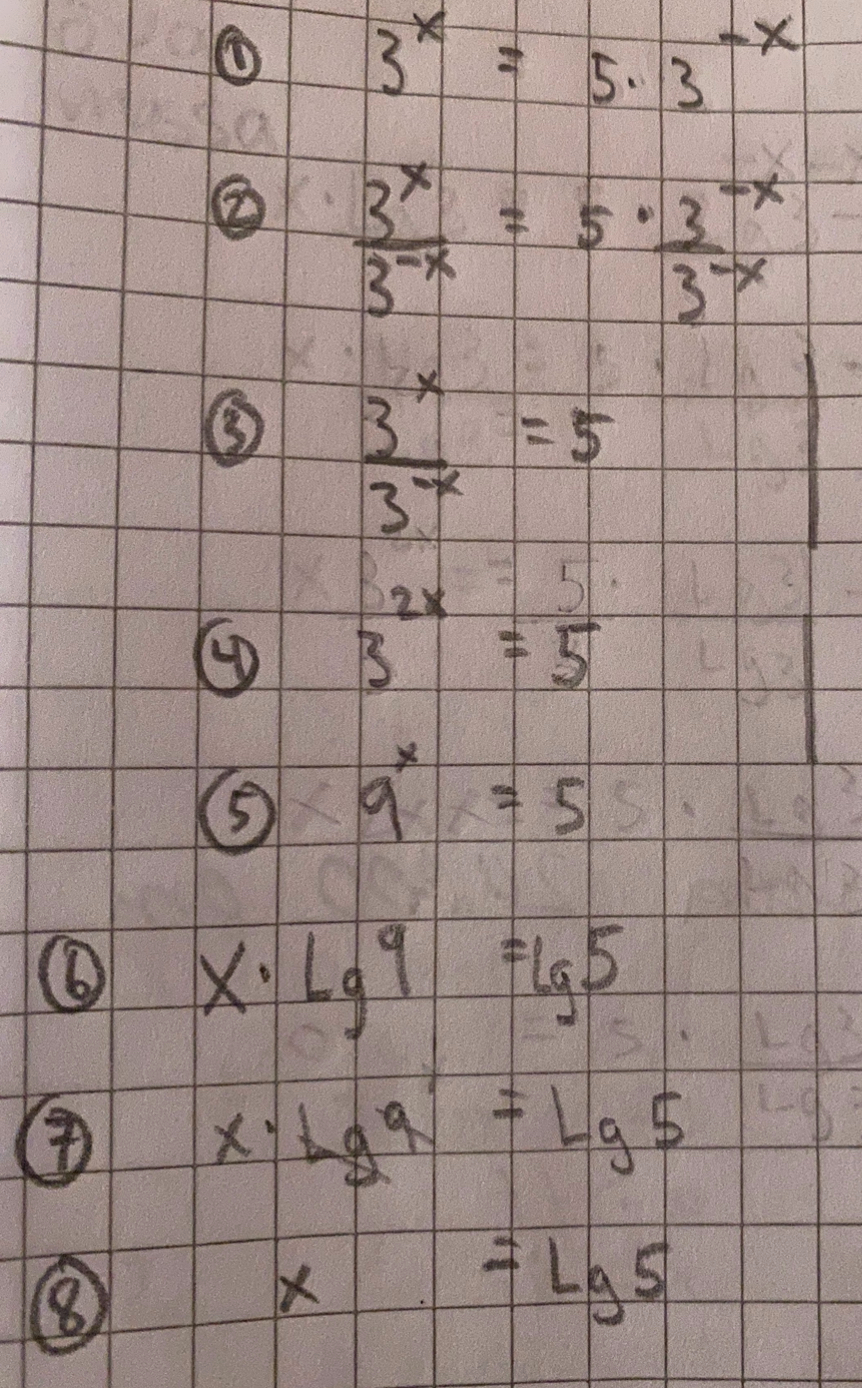
men blir något förvirrad för
jag har ju 2x dvs 2st x i steg 3. & de 2 x:en flyttas till exponenten så då får jag ju 2x där så vad händer med det andra x:et? Liksom från
steg 4) till steg 5) v.l tänker jag?
Du verkar vilja stryka saker som ser krångliga ut, utan att det stämmer matematiskt. Steg 6 är rätt. Hur tänker du för att komma till steg 7 och 8?
Du har rätt, är rätt förvirrad för tillfället..
Men kanske att jag delar så Lg9 hamnar under Lg5 och så har jag svaret exakt?
Typ:
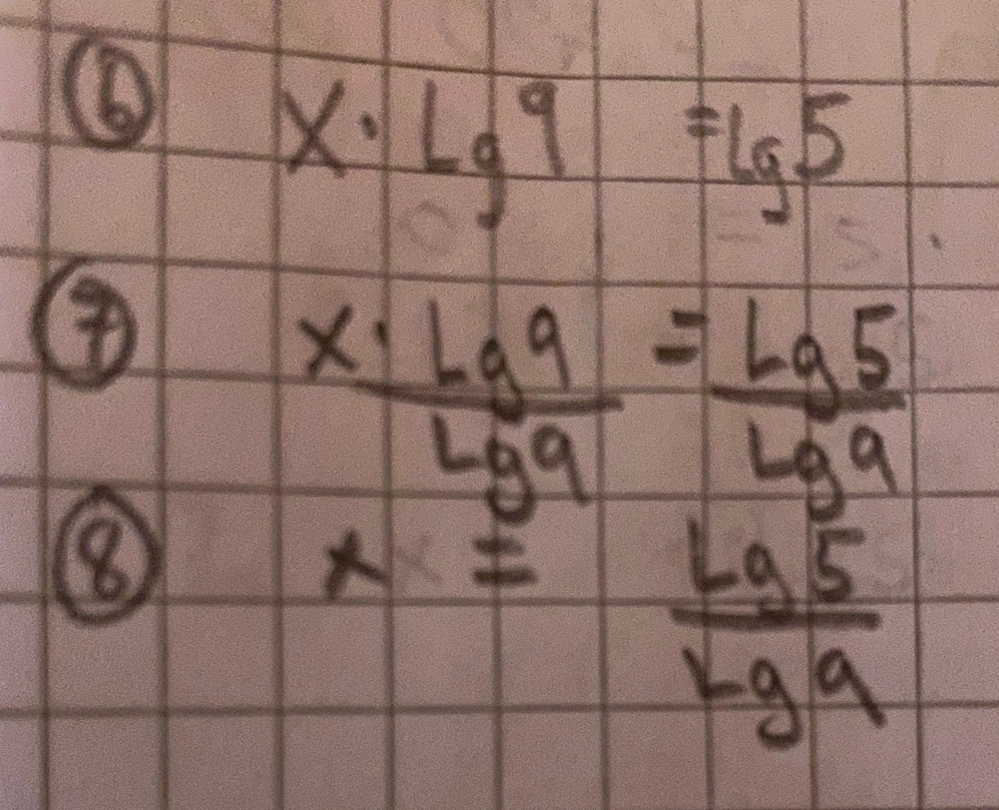
Naturens skrev:men blir något förvirrad för
jag har ju 2x dvs 2st x i steg 3. & de 2 x:en flyttas till exponenten så då får jag ju 2x där så vad händer med det andra x:et? Liksom från
steg 4) till steg 5) v.l tänker jag?
Och ja, du har löst den korrekt och exakt =)
Tack för all hjälp
Naturens skrev:[...]
jag har ju 2x dvs 2st x i steg 3. & de 2 x:en flyttas till exponenten så då får jag ju 2x där så vad händer med det andra x:et? Liksom från
steg 4) till steg 5) v.l tänker jag?
EDIT - lite sen på bollen, men nu har jag skrivit allt så jag låter det stå.
Steg 3:
Enligt potenslagen så blir VL , vilket är lika med
Steg 4:
VL kan skrivas . Enligt potenslagen så kan VL skrivas , vilket är lika med
Steg 5:
Hängde du med på det?
===========
Kommentar: Du behöver inte göra denna omskrivning. Du kan lika gärna logaritmera bägge led i steg 4.
Du får då , vilket ger .
=≈≈≈==========
Kommentar på fortsättningen:
Om du tycker att logaritmuttrycken förvirrar så kan du, som jag tidigare tipsat om, tillfälligt byta ut dem mot något enklare.
Exempel:
Ersätt tillfälligt med och med .
Ekvationen blir då , vilket efter division med blir .
Nu kan du byta tillbaka från och och du får då lösningen .
=======
Kommentar på hur du skriver logaritmuttryck.
Jag rekommenderar att du skriver parenteser kring argumentet i dina logaritmuttryck, dvs att du skriver istället för
Tack jag måste försöka komma ihåg det



