Lös ekvationen
Hej :)
Jag har en uppgift som lyder:
Lös ekvationen: Sin2x = 0.875. Svara i radianer
Det jag gjort:
Nu ska jag omvandla till radianer
Nu fastnar jag, för jag tänker att man bör svara i exakt form hur får jag fram det om det jag gjort nu är rätt?
Edit: slarvfel
Såvitt jag kan se går det inte att hitta en exakt lösning. 0.53 radianer blir nog bra.
...och så ska du hitta andra hälften av lösningarna...
Tänkte du på att sinus alltid ger två fall dvs
Jo, det var att det finns två svar Bubo tänkte på men det andra svaret är inte -30,5 grader. Det är cosinus som ger de två resultaten.
Men varför håller du på med grader i denna uppgift? Du blandar dessutom grader och radianer när du sätter upp svaret. Eftersom man kan konstatera att detta inte är ett känt värde på sinus kommer vi inte att kunna svara exakt och därmed ställer vi in räknaren på radianer och tar ut värdet direkt. Om det inte står "svara exakt" i uppgiften är ett decimaltal ett acceptabelt svar när du skall svar i radianer.
Standardfråga 1a: Har du ritat? (Enhetscirkeln, alltså.)
AndersW skrev:Jo, det var att det finns två svar Bubo tänkte på men det andra svaret är inte -30,5 grader. Det är cosinus som ger de två resultaten.
Men varför håller du på med grader i denna uppgift? Du blandar dessutom grader och radianer när du sätter upp svaret. Eftersom man kan konstatera att detta inte är ett känt värde på sinus kommer vi inte att kunna svara exakt och därmed ställer vi in räknaren på radianer och tar ut värdet direkt. Om det inte står "svara exakt" i uppgiften är ett decimaltal ett acceptabelt svar när du skall svar i radianer.
Hur lång gör jag rätt? hit?

Nej, du skall ställa om räknaren till radianer med en gång. Det finns ingen anledning att "mellanlanda" på grader.
Dessutom har du bara fått med hälften av alla lösningar. Använd enhetscirkeln, så hittar du den andra hälften också.
Så långt som du har markerat är det korrekt. Man kan även säga att nästa rad är korrekt, även om jag inte skulle göra så utan skriva:
Och så var det detta med det andra svaret...
om jag kollar på enhetscirkeln bör det bli -1.06 + n * 2 ?
Det andra svaret alltså.
Edit: slarvfel
Nej, det är det samma som du angett tidigare. Det är cosinus som ger svaren +-v.
Sinus läses av på y-axeln så den andra vinkeln blir?
Nej - det skulle det bli om det var cos(2x) det handlade om. Använd enhetscirkeln! För mig underlättar det att tänka på att cosinus och sinus kommer i alfabetisk ordning, precis som x och y, d v s cosinus är på x-axeln och sinus på y-axeln. Alltså skall du titta vilka två värden på enhetscirkeln som har y-värdet 0,875.
Nej, var fick du det ifrån? Sinus för 70 grader är ca 0.94
Bubo skrev:Nej, var fick du det ifrån? Sinus för 70 grader är ca 0.94
läste av fel, då?
Ett tips:
(radianer)
Jag förstår inte hur jag ska göra..
sin 2x=0,875
Låt oss kalla 2x för a så får du
sin(a)=0,875 Rita nu in detta i en enhetscirkel och ladda upp hit.
Vi bör hålla oss till en enhet för vinkel, antingen grader eller radianer. Det blir rörigt att blanda dem.
Japp, sinus för 61 grader och sinus för 119 grader är 0.875. Kommer du vidare nu?
119 grader är ett halvt varv minus 61 grader. Ser du sambandet i enhetscirkeln?
joculator skrev:sin 2x=0,875
Låt oss kalla 2x för a så får dusin(a)=0,875 Rita nu in detta i en enhetscirkel och ladda upp hit.

Bubo skrev:Vi bör hålla oss till en enhet för vinkel, antingen grader eller radianer. Det blir rörigt att blanda dem.
Japp, sinus för 61 grader och sinus för 119 grader är 0.875. Kommer du vidare nu?
119 grader är ett halvt varv minus 61 grader. Ser du sambandet i enhetscirkeln?
Ne tyvärr.
a är nog rätt y, men det är punkter _på_ enhetscirkeln som efterfrågas. Hitta punkter på cirkeln som har y = a.
Rita en ny enhetscirkel. Låt origo vara exakt där två linjer korsar varandra. Låt cirkeln ha radien 10 rutor och rita ut x-och y-axeln. Lägg in bilden här när du har gjort detta, så skall vi gå vidare därifrån.
Smaragdalena skrev:Rita en ny enhetscirkel. Låt origo vara exakt där två linjer korsar varandra. Låt cirkeln ha radien 10 rutor och rita ut x-och y-axeln. Lägg in bilden här när du har gjort detta, så skall vi gå vidare därifrån.
Den får duga. Markera nu den räta linjen i samma koordinatsystem.
Smaragdalena skrev:Den får duga. Markera nu den räta linjen i samma koordinatsystem.
Dra räta linjer från origo till de båda punkter där den räta linjen y=0,875 korsar enhetscirkeln.
Smaragdalena skrev:Dra räta linjer från origo till de båda punkter där den räta linjen y=0,875 korsar enhetscirkeln.

Mät (med en gradskiva) vinkeln mellan positiva x-axeln och de båda räta linjerna. I en perfekt värld skulle du ha en "radianskiva" istället, men i brist på sådan får vi räkna om det.
Smaragdalena skrev:Mät (med en gradskiva) vinkeln mellan positiva x-axeln och de båda räta linjerna. I en perfekt värld skulle du ha en "radianskiva" istället, men i brist på sådan får vi räkna om det.
Jag har ingen gradskiva..
Skriv ut den här, den har både grader och radianer:
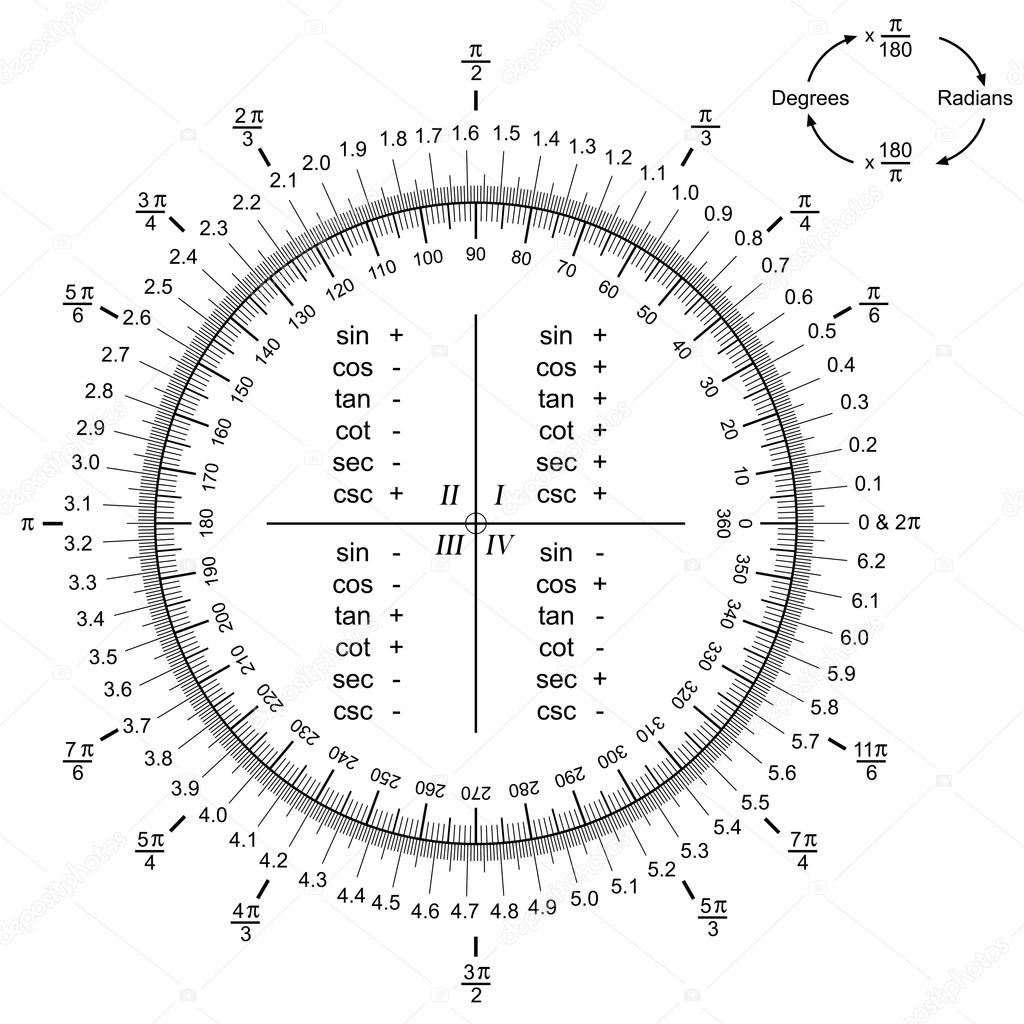
Jag har alltså
Nej, då skulle y-värdet ha varit 0,86602540378443864676372317075294, och du skall ha y=0,875. Nära, men inte samma.
Du skull e kunna använda din räknare istället: Ställ in räknaren på radianer och ta reda på vilka vinklar som motsvar sinus-värdet 0,875. Lägg märke till att du har en lösning i första och en in andra kvadranten.
Smaragdalena skrev:Nej, då skulle y-värdet ha varit 0,86602540378443864676372317075294, och du skall ha y=0,875. Nära, men inte samma.
Du skull e kunna använda din räknare istället: Ställ in räknaren på radianer och ta reda på vilka vinklar som motsvar sinus-värdet 0,875. Lägg märke till att du har en lösning i första och en in andra kvadranten.
sin (0.875) = 0.7675435022
Smaragdalena skrev:Skriv ut den här, den har både grader och radianer:
Snygg, men den är inte cirkulär hos mig.
Konstigt, för mig är den åtminstone så rund att jag inte kan säga om den skulle vara som en nolla eller tillplattad på andra hållet.
Hur ska jag sammanfatta denna tråd, för att komma fram till ett svar?
efter detta började vi kolla på enhetscirkeln med andra värden från . Vilket av dem ska jag använda för att slutföra uppgiften?
Nej, sin(0.875) har ingenting med denna uppgift att göra.
Hur ska jag göra för att slutföra denna uppgift nu?
Jag började med:
Bubo skrev:Nej, sin(0.875) har ingenting med denna uppgift att göra.
Då har jag missuppfattat. hur ska jag använda 0.53? kolla i enhetscirkeln?
Bubo måste blanda ihop dina trådar.
eller
Kan du fortsätta härifrån?
Så du tänkte smaragdalena?
Sista lösningen x = 1.04 ligger inte inom enhetscirkel och borde därför gå bort?
MonaV skrev:Sista lösningen x = 1.04 ligger inte inom enhetscirkel och borde därför gå bort?
Vad menar du med det? Det står inget annat än att du skall ge samtliga kösmingar. Och vad menar du med att värdet inte ligger inom enhetscirkeln?
Tänkte att radien är 1 i enhetscirkeln, men tänkte då fel. hur går jag vidare?
MonaV skrev:Sista lösningen x = 1.04 ligger inte inom enhetscirkel och borde därför gå bort?
Här blir det lite sammanblandning av variabelnamn.
Ekvationen lyder sin(2x) = 0.875.
Det betyder att x betecknar en vinkel.
Då ska vi inte döpa den horisontella axeln i enhetscirkeln till x för det förvirrar bara.
Yngve skrev:MonaV skrev:Sista lösningen x = 1.04 ligger inte inom enhetscirkel och borde därför gå bort?
Här blir det lite sammanblandning av variabelnamn.
Ekvationen lyder sin(2x) = 0.875.
Det betyder att x betecknar en vinkel.
Då ska vi inte döpa den horisontella axeln i enhetscirkeln till x för det förvirrar bara.
Tack då förstår jag hur jag kunde tänka fel!!
MonaV skrev:Så du tänkte smaragdalena?
Är detta svaret?
Nej, eftersom jag inte förstår vad det är du vill ha fram är det i alla fall inget bra svar.
Svaret skall se ut ungefär som "Svar: eller eller " fast med rätt siffror (jag hittade bara på siffrorna).
Smaragdalena skrev:Nej, eftersom jag inte förstår vad det är du vill ha fram är det i alla fall inget bra svar.
Svaret skall se ut ungefär som "Svar: eller eller " fast med rätt siffror (jag hittade bara på siffrorna).
Jag vill ha fram svaret men förstår inte vad jag ska göra längre.
Att bara vilja "ha fram svaret" är ingen bra idé - det du borde vilja är FÖRSTÅ vad du gör och varför du gör det. Börja från början och lös uppgiften ändra tills du kommer fram till svaret. Antingen klarar du att göra det, och då har du lärt dig hur man gör, eller också klarar du inte av det, och då kan du fråga ännu mer.
Jag förstår hela vägen till dit jag kommit nu (det jag trodde va svaret). Jag kan lösa om den men kommer fastna på samma ställe.
Nu vet jag inte vad jag mer kan göra?
Om jag ritar upp den grafiskt finns dessa skärningar med + 2 st till, är det dessa jag ska hitta?
Vad är det jag inte ser som fattas i denna uppgift? Jag får verkligen inte till den :(
MonaV, det står i Pluggakutens regler att man skall vänta åtminstone 24 timmar innan man bumpar sin tråd. /moderator
Smaragdalena skrev:MonaV, det står i Pluggakutens regler att man skall vänta åtminstone 24 timmar innan man bumpar sin tråd. /moderator
Hade inte en tanke på att jag gjorde så, tog bara upp där jag sluta igår..
Vilken vinkel är sådan att sinus för vinkeln är 0.875? Med räknare hittar man 1.06 radianer. När man tittar i enhetscirkeln ser man också att 2.08 radianer är en sådan vinkel.
Rita en enhetscirkel och övertyga dig om att sin(v) = sin(etthalvtvarv - v)
1.06 rad plus ETT eller TVÅ eller TRE... varv är också lösningar. Det ger oss
2x = 1.06 + N * 2pi. som blir x= 0.53 + N * pi
och detta är ena hälften av lösningarna.
Klart. (Halvvägs. Andra hälften gör du klart på samma sätt)
Bubo skrev:Vilken vinkel är sådan att sinus för vinkeln är 0.875? Med räknare hittar man 1.06 radianer. När man tittar i enhetscirkeln ser man också att 2.08 radianer är en sådan vinkel.
Rita en enhetscirkel och övertyga dig om att sin(v) = sin(etthalvtvarv - v)
1.06 rad plus ETT eller TVÅ eller TRE... varv är också lösningar. Det ger oss
2x = 1.06 + N * 2pi. som blir x= 0.53 + N * pi
och detta är ena hälften av lösningarna.
Klart. (Halvvägs. Andra hälften gör du klart på samma sätt)
Hur kan man se 2.08 rad i enhetscirkeln? Kanske väldigt dum fråga, men allt detta är väldigt nytt för mig.
Andra hälften var
Edit: slarvfel
Har du verkligen ritat?
Allra första bilden på https://sv.m.wikipedia.org/wiki/Enhetscirkel
visar en punkt på enhetscirkeln med y-koordinat sin(t). Rita ut den andra punkten på enhetscirkeln som har samma y-koordinat.
Då ser du nog sambandet.
Japp jag har ritat!

Om jag har förstått dig rätt, så vill du att jag ska se varför det finns två lösningar? :)
Edit: Enhetscirkeln är inte perfekt men jag förstår syftet:)
Ja. Snyggt.
Nu ser du ATT det finns två punkter "på samma höjd", med samma y-koordinat. De ligger symmetriskt på var sin sida om y-axeln, det ger dig sambandet mellan vinklarna.
För den vänstra punkten är x-koordinaten inte cos(t), utan -cos(t).
Bubo skrev:Ja. Snyggt.
Nu ser du ATT det finns två punkter "på samma höjd", med samma y-koordinat. De ligger symmetriskt på var sin sida om y-axeln, det ger dig sambandet mellan vinklarna.
För den vänstra punkten är x-koordinaten inte cos(t), utan -cos(t).
Ja just de, de glömde jag bort! Min andra hälft är väl fortfarande det jag räknat ut algebraiskt?dvs x = 1.04 +n *
Trots att de är på samma höjd för y-värdet så är dess x-värden inte de samma? Eller blev det knasigt? :)
Jag blir inte klok på vad du gör rätt och vad du har missuppfattat.
Kan du repetera hela lösningen, med en snygg figur? De flesta av dina svar innehåller någon felaktighet och jag vet inte hur mycket av det som bara är slarv.
Ne allt är jätte rörigt!
Jag börjar om:

Enhetscirkeln visar två lösningar!
Alltså
Edit: slarvfel
Ja, det är rätt.
Din figur har fortfarande ett teckenfel i den vänstra punktens x-koordinat.
Bubo skrev:Ja, det är rätt.
Din figur har fortfarande ett teckenfel i den vänstra punktens x-koordinat.
Kanon! :)
Jag ska rätta till det :)
Tack så mycket :)
Smaragdalena skrev:Konstigt, för mig är den åtminstone så rund att jag inte kan säga om den skulle vara som en nolla eller tillplattad på andra hållet.
Det är min skärm som är konstig!
Hej! Jag behöver hjälp med att förstå varför man skriver n * 2π när man gör ekvationen .
Hittade svaret, moderator kan ta bort inlägget.








