Lös differentialekvationen:

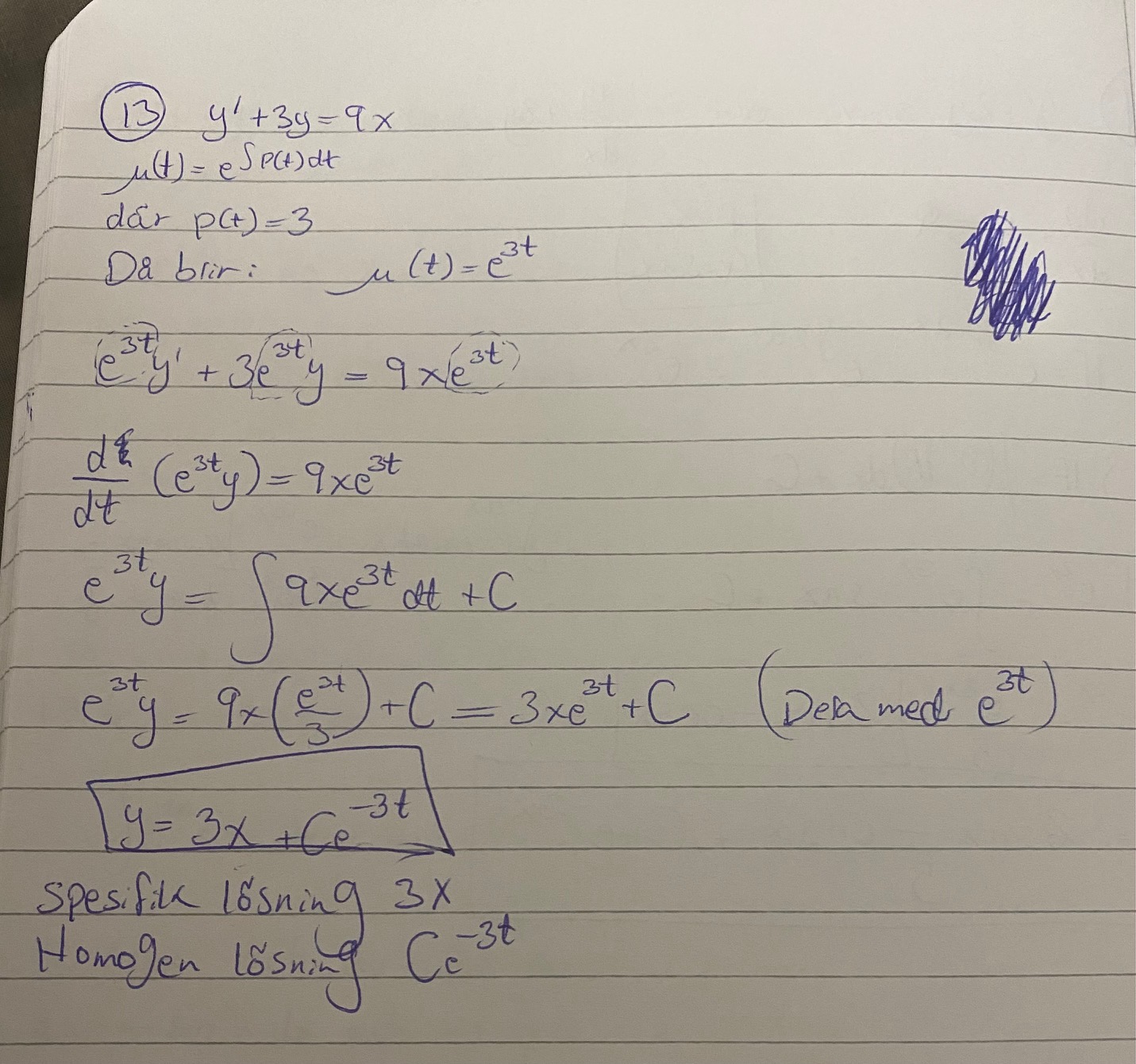
Hej!

Först en fråga. Det ingick i uppgiften att diffekvationen skulle lösas med integrerande faktor, eller hur?

Alternativ1 kommer du fram till rätt svar på, men du gör ett tankefel på vägen dit. Samma tankefel gör att du kommer fram till fel svar i alternativ2.

Tankefelet du gör är att du ska söka en lösningsfunktion y som beror av x. Det finns ingen variabel t (vad vi vet iallafall). y' betyder i det här fallet underförstått y'(x).

Så den integrerande faktorn är $e^{\int 3dx}$ (inte $e^{\int 3dt}$), vilket tex betyder att i ditt lösningsalternativ2 så blir det inte

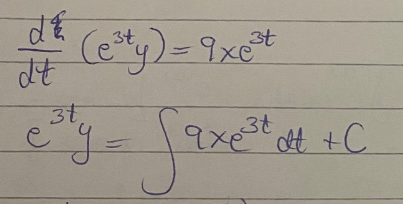utan 

$$\begin{gathered} \frac{d}{dx}\left(e^{3x}y\right)=9x{e}^{3x} \\ {e}^{3x}y=\int 9x{e}^{3x}dx + C \end{gathered}$$

Kommer du vidare?

Det stod bara:

Lös differentialekvationen: y'+3y=9x 

ingenting om (med integrerande faktor)

JohanF skrev:

Hej!

Först en fråga. Det ingick i uppgiften att diffekvationen skulle lösas med integrerande faktor, eller hur?

Alternativ1 kommer du fram till rätt svar på, men du gör ett tankefel på vägen dit. Samma tankefel gör att du kommer fram till fel svar i alternativ2.

Tankefelet du gör är att du ska söka en lösningsfunktion y som beror av x. Det finns ingen variabel t (vad vi vet iallafall). y' betyder i det här fallet underförstått y'(x).

Så den integrerande faktorn är $e^{\int 3dx}$ (inte $e^{\int 3dt}$), vilket tex betyder att i ditt lösningsalternativ2 så blir det inte

utan 

$$\begin{gathered} \frac{d}{dx}\left(e^{3x}y\right)=9x{e}^{3x} \\ {e}^{3x}y=\int 9x{e}^{3x}dx + C \end{gathered}$$

 

Kommer du vidare?

Men blir svaret då: y=3x+$C{e}^{-3x}$( Som i lösning försök 2)

eller bli svaret: y= 3x- 1+$\frac{C_1}{e^{3x}}$(Som i lösning försök 1)

Du kommer fram till rätt svar i alternativ1 (Att prova att sätta in lösningen i diffekvationen brukar vara det enklaste sättet att kontrollera ett svar). Men du gör samma tankefel på vägen till lösningen, i både alt1 och alt2.

shadosi skrev:

Det stod bara:

Lös differentialekvationen: y'+3y=9x 

ingenting om (med integrerande faktor)

Med ditt alternativ1 blir det en vanlig homogen diffekvation att lösa, y'+3y=0. Lösningen till den är en tabellerad standardlösning. Men såklart kan du lösa den homogena diffekvationen med integrerande faktor om du vill.