Logaritmregler
Läraren från denna video visar två exempel om logaritmer, varför delar han inte log10 i första exemplet, och varför gör han det i andra exemplet?
Som en slags följdfråga: Vad är det för skillnad som gör att man inte behöver dela i första exemplet, kontra varför man behöver det i andra?
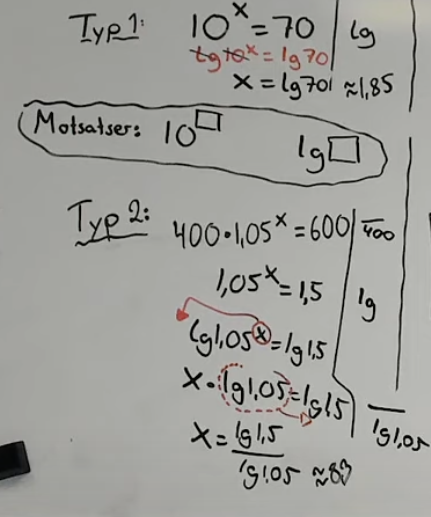
Tack för svar.
Hejsan!
Principen är egentligen det samma för båda dessa fall!
Häng med på denna tankegången:
Typ 2:
Här utnyttjar vi logaritmlagarna som säger att vi alltså kan "flytta ned x:et" och sätta multiplikation framför och sedan dividerar vi för att lösa ut x. Den regeln tror jag du är med på, visst?
I typ 1 gör vi egentligen samma sak (bara att man hittat en liten genväg)
här kommer vi till det finurliga...
lg x kan man definiera som "talet vi ska upphöja 10 med för att få x" dvs blir lg 100 = 2 eftersom att 10^2 = 100
Detta gör ju att lg 10 måste vara 1 eftersom att 10^1 = 10
När vi skriver lg 10 är det alltså samma som att skriva 1 vilket gör att man kan stryka lg 10 när det gäller MULTIPLIKATION. vi fortsätter med vår typ 1
För att sammanfatta:
Vi använder oss av samma lg lagar i båda fallen men istället för att vid typ 1 skriva ut hela långa processen där vi förenklar lg 10 till 1 så stryker vi lg och 10 när de hamnat bredvid varandra. Vi är lite lata och smarta eftersom att resultatet blir samma.
Så står det
då dividerar du båda leden med 400. Logaritmerar båda leden och tar genvägen - stryker lg och 10 eftersom du är lat och smart och numera VET att det är detsamma som 1. Och varför dividera med 1... det är ju onödigt slöseri med tid :)
Hängde du med? Några otydligheter
Fantastiskt svar, tack så jättemycket!
Så det går att säga att man gör det i båda typerna, bara att det är överflöd att skriva ut det i ena, men nödvändigt i andra?
Jag skulle ha skrivit ut 10lg på båda sidor i exempel 2 också, det passar min hjärna bättre.



