Logaritm
 är min min lösning tydlig och motiverad?
är min min lösning tydlig och motiverad?

Du gör fel på första raden, när du logaritmerar måste du ta med hela ledet, inte ta varje term för sig.
Alltså
ln(ex+2e2x) = ln(6)
Det är nog lättare att sätta in x = ln(2) i ursprungsekvationen och visa att VL = HL
eln(2) + e2ln(2) och förenkla härifrån för att
förhoppningsvis komma fram till värdet 6
Jag hänger inte med på hur jag ska fortsätta ifrån ln(ex+2e2x) = ln(6)
Eller var bara första raden fel men resten ok?
Likaså hur gör man om man skriver om till eln(2) + e2ln(2) ?
Biorr skrev:Jag hänger inte med på hur jag ska fortsätta ifrån ln(ex+2e2x) = ln(6)
Eller var bara första raden fel men resten ok?
Du ska inte fortsätt härifrån, det bli alldeles för besvärligt. Jag ville bara visa att du gjort fel och hur du skulle ha gjort för att inte göra formellt fel.
Eftersom första raden var fel blir resten oxå fel.
Likaså hur gör man om man skriver om till eln(2) + e2ln(2) ?
Titta på räkneregler för logaritmer det finns nog något som passar.
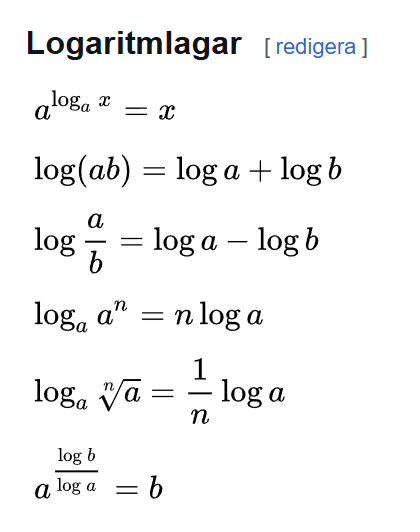
 såhär med hjälp av denna lag?
såhär med hjälp av denna lag?

Var kommer ln2 från i Högerledet på rad 2?
Jag missförstod nog infot.
”Det är nog lättare att sätta in x = ln(2) i ursprungsekvationen och visa att VL = HL”
ska det vara bara 6?
så blir det 6=6
Just det, och om vl = hl så är lösningen korrekt.
 jag kunde göra eln(2) + e2ln(2) =6 , bara för att ja visste att x=ln2.
jag kunde göra eln(2) + e2ln(2) =6 , bara för att ja visste att x=ln2.
vad hade hänt om man inte visste om x=ln2?
Då hade man fått lösa ursprungsekvationen


