Ljusets diffraktion
Har lite problem med följande uppgift:
En laserstråle med våglängden 632,8 nm belyser en skärm med en hög spalt med
bredden 50 μm.
a. Beräkna approximativt i vilken vinkel det första maximum utanför centralmaxi-
mum inträffar.
b. Beräkna kvoten mellan intensiteterna i de bägge maxima.
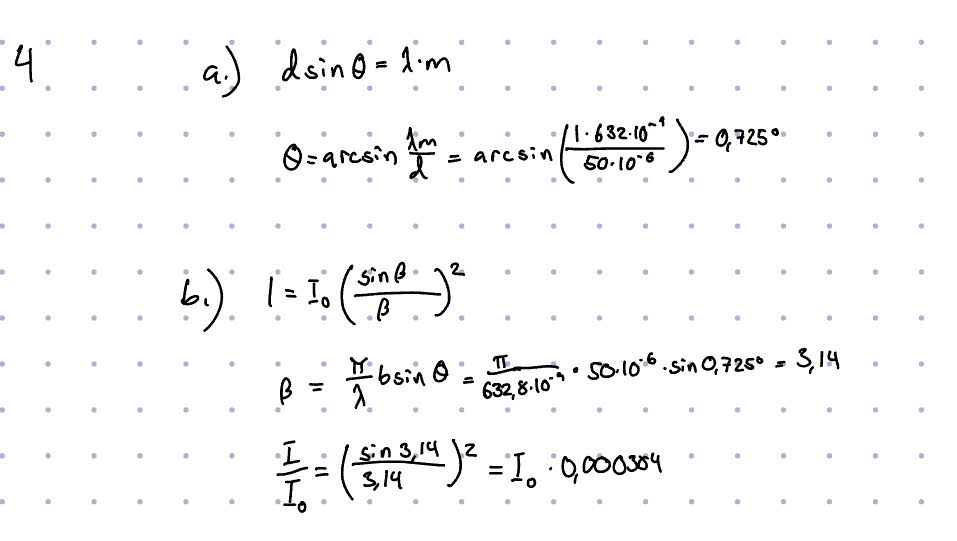
Känns som att jag är på rätt väg men kvoten känns också orimligt liten, hur ska jag gå till väga?
Du har använt formeln för maximum för diffraktion från en dubbelspalt. Samma formel gäller inte för en enkelspalt. Vad gäller där?
Förlåt, det du använt är förstås formeln för intensitetsminimum. Sen har du i b) räknat i grader istället för radianer - annars skulle du fått storleksordningen . Och att du inte kom ner till 0 beror på avrundningsfel.
Funkar det inte att använda grader snarare än radianer så länge jag håller mig till grader?
Sen tror jag det stora problemet är att jag i a) räknat för minimum snarare än maximum, hur bör jag gå till väga för att räkna på maximum i enkelspalt?
Förstår inte riktigt heller varför jag skulle vilja komma ner till 0?
Slutligen märker jag att det smitigt in ett I0 för mycket i sista raden, den framför 0,000304 ska inte vara där :)
Funkar det inte att använda grader snarare än radianer så länge jag håller mig till grader?
Jo, om du strikt håller dig till grader så går det. Men det du tagit fram (3.14) är uttryckt i radianer och inte grader (talet 3.14 kanske får dig att reagera).
hur bör jag gå till väga för att räkna på maximum i enkelspalt?
För att hitta maximum får du fundera på när har maximum.
Förstår inte riktigt heller varför jag skulle vilja komma ner till 0?
Du "vill" väl kanske inte nå 0, men eftersom du (felaktigt) använde formeln för intensitetsminimum, så borde ju resultatet blivit 0. har ju sitt minimum när , och antar då .
edwardramberg skrev:Funkar det inte att använda grader snarare än radianer så länge jag håller mig till grader?
Men det är mycket lättare med radianer, särskilt vid så små vinklar där
Då går det utan miniräknare.
haraldfreij skrev:Du "vill" väl kanske inte nå 0, men eftersom du (felaktigt) använde formeln för intensitetsminimum, så borde ju resultatet blivit 0. har ju sitt minimum när , och antar då .
Nej, centralt maximum.
Därför har man definierat sinc-functionen där sinc(x) = sin(x)/x förutom för x=0 där sinc(0) = 1.
Men det finns också en definition med π : https://sv.wikipedia.org/wiki/Sinc-funktionen
Pieter Kuiper skrev:Nej, centralt maximum.
Fast jag skrev , inte


