Ljudets hastighet och interferens

Kan du några samband mellan vägskillnad och våglängden när det kommer till interferens? För formeln du angivit så märker ser du nog att det är våglängden $\lambda$ vi behöver för att få hastigheten $v$. Frekvensen är ju angiven i uppgiften. 

Ljud i fas förstärker varandra och ljud i motfas släcker ut varandra. Det innebär att där avståndet till respektive ljudkälla är lika långt eller med en skillnad på en jämn multipel av våglängden på ljudet har du ett maxima. 

Det kan du kanske se om du tänker dig ljudvågorna som cirkulära vågor med start i högtalarna. Tänk dig att man kastar en sten i vatten så kanske du ser dem framför dig. 

Sen är det "bara" geometri. Är du med på det? 

Jag räknade ut vägskillnaden:

Sambandet jag hittade var:△s​=kλ

Men vad är K och vad motsvarar den?

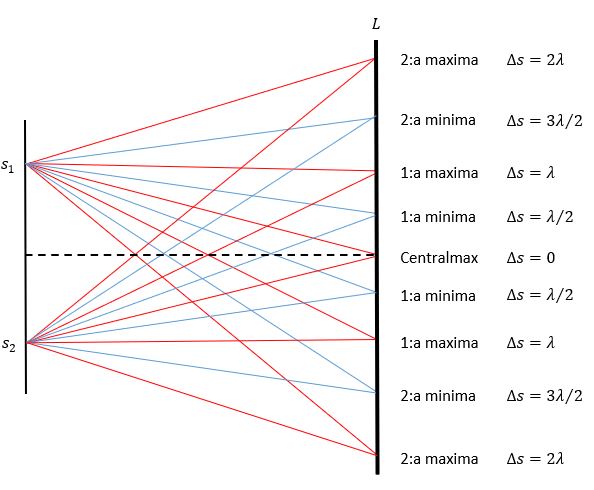
k är vilket max det är (se bild). I ditt fall här är det 1:a så sätt in k=1 och lös ut $\lambda$.

Hur läser du av bilden? Eftersom ifall jag jämför bilden jag ritade med denna bild blir K = 2 enligt mig?

Skalan är inte samma för alla fall. När våglängden varierar så varierar även avståndet mellan maxima. Från uppgiften kan vi, även om det är lite oklart, förstå att det är 1:a max.

Jag har löst uppgiften men skulle gärna vilja förstå varför man använder 1:a maxima, har googlat runt lite men förstår fortfarande inte

Vad får dig att tro att man inte skulle använda det? Bilden jag skickade visade bara generellt vad som gäller. Skulle man rita ut alla max och min på din bild skulle de vara längre ifrån vara varandra.

En anledning är ju också att du ritat väldigt grovt och icke-skalenligt. Enligt din bild är 6 m nästan lika långt som 0,6 m. Och det stämmer ju inte. 

Peter.kalle skrev:

Jag har löst uppgiften men skulle gärna vilja förstå varför man använder 1:a maxima, har googlat runt lite men förstår fortfarande inte

Googla inte, läs uppgiften istället:

Två små högtalare är uppställda sida vid sida med ett avstånd från varandra av 60 cm. En elev befinner sig på mittpunktsnormalen till sträckan mellan högtalarna och 6,0 m från dessa. Högtalarna är kopplade till samma tongenerator som avger en ton med frekvensen 5,7 kHz. När eleven flyttar sig 0,60 m rakt åt höger hör han ett nytt ljudmaximum. Bestäm ljudets hastighet.

Om det hade varit ett annat maximum däremellan borde man ha skrivit det (fast det kunde ha varit tydligare skrivet).

Okej tack så mycket för era svar, jag förstår nu!

Jag räknade ut såhär och fick fram 285m/s som ljudest hastighet vilket låter rimligt?

△s​ = kλ

λ =△s​/k

0,05/1 = 0,05 = λ

v = f * λ

5,7 * 10³ * 0,05 = 285m/s

Din skiss av vägskillnaden stämmer inte.

Den ska vara skillnaden i sträcka från de båda högtalarna till punkten P, se bild.

Vägskillnaden råkar bli densamma i detta fallet, men det är ändå viktigt att få till illustrationen rätt.

Ditt värde på ljudhastigheten stämmer inte heller, men det beror på att du gör alltför stora avrundningar när du tar fram s₁ och s₂. Eftersom detta närmevärde multipliceras med 5 700 på slutet så blir felet stort.

Gör gärna en rimlighetskontroll genom att googla "Ljudhastighet i luft".

== Kommentar till den otydliga uppgifftslyfelsen ==

Sedan tycker jag att man egentligen bör tolka uppgiftslydelsen

En elev befinner sig på mittpunktsnormalen till sträckan mellan högtalarna och 6,0 m från dessa.

som att sträckorna AC och BC båda är 6,0 meter, eftersom "dessa" refererar till högtalarna.

Om de istället menade avståndet till sträckan mellan högtalarna så borde de ha skrivit "denna". 

Räkna gärna även på det omtolkade fallet.

Det stämmer, jag gjorde mindre avrundningar och fick fram att ljudets hastighet är 339,89 m/s vilket stämmer med verkligheten.

Räknade ut på det omtolkade fallet men det skiljde sig väldigt lite, fick 340,3 m/s

Gjorde om mina beräkningar så att sträckorna blir rätt (Som du ritade) så nu ska allt stämma.

Tack för hjälpen!