Lite tips tack.
Hej.
Skulle vara tacksam om någon bara kunde ge mig en ledtråd för hur man tar sig an följande uppgift, vill gärna komma på det själv tack.
(Jag har fyllt i de X:en, Y:en och Zätat själv, det kanske inte ens är korrekt men det ser ut att vara två likbenta trianglar.)
Jag skulle kunna namnge alla vinklar som jag hittar och utnyttja att jag vet att summan av en triangels vinklar är 180. Därmed så kanske jag kan få fram vinklarnas värde genom ekvationer?
Det spelar ingen roll om de är likbenta. Titta på mittenfiguren, hur stor är dess vinkelsumma? Notera sedan att figuren är sammansatt av trianglar, med ett hörn i mittenfiguren.
Smutstvätt skrev:Det spelar ingen roll om de är likbenta. Titta på mittenfiguren, hur stor är dess vinkelsumma? Notera sedan att figuren är sammansatt av trianglar, med ett hörn i mittenfiguren.
Mittfiguren har vinkelsumman 360 + 180 Sedan så är det 5 trianglar runt omkring
Smutstvätt skrev:Det spelar ingen roll om de är likbenta. Titta på mittenfiguren, hur stor är dess vinkelsumma? Notera sedan att figuren är sammansatt av trianglar, med ett hörn i mittenfiguren.
Kollade på lösningen och mittfigurens vinkelsumma var inte nödvändig för att komma fram till en lösning.
Facit använder sig utav yttervinkelsatsen på följande sätt: (Orkade inte vänta längre)
Visa hur du menade.
Hmm, intressant. Det är ett smidigare sätt att göra det på, men min metod är liknande:
Vi kan konstruera figuren genom att låta fem trianglar överlappa lite:
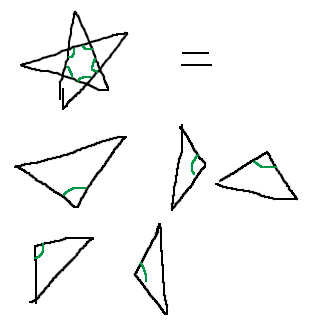 (De gröna vinklarna är vinklarna i pentagonen, övriga vinklar blir stjärnans uddar)
(De gröna vinklarna är vinklarna i pentagonen, övriga vinklar blir stjärnans uddar)
När vi sätter ihop dessa får vi vinklarna i pentagonen i mitten av stjärnan. Den har vinkelsumman 540 grader (vilket kan visas, om det behövs). Trianglarna har tillsammans vinkelsumman 5·180°, men varje vinkelspets är räknad två gånger, vilket ger att vinkelsumman för spetsarna är grader.
Här finns en drös med olika lösningar på detta problem:




